题目内容
已知函数y=sin(
-
x)
(Ⅰ)求该函数的周期,并求函数在区间[0,π]上的值域;
(Ⅱ)求该函数在[-2π,2π]上的单调增区间.
| π |
| 3 |
| 1 |
| 2 |
(Ⅰ)求该函数的周期,并求函数在区间[0,π]上的值域;
(Ⅱ)求该函数在[-2π,2π]上的单调增区间.
考点:正弦函数的单调性,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)由题意易得周期,由x的范围可得
-
x的范围,进而可得;(Ⅱ)原函数的增区间即为y=sin(
x-
)的减区间,令2kπ+
≤
x-
≤2kπ+
,解不等式和[-2π,2π]取交集即可.
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:
解:(Ⅰ)由题意函数的周期T=
=4π,
∵x∈[0,π],∴
-
x∈[-
,
],
∴sin(
-
x)∈[-
,
],
即函数在区间[0,π]上的值域为[-
,
];
(Ⅱ)原函数可化为y=-sin(
x-
),
原函数的增区间即为y=sin(
x-
)的减区间,
令2kπ+
≤
x-
≤2kπ+
,
解得4kπ+
≤x≤4kπ+
,k∈Z,
令k=0,可得
≤x≤
,
令k=-1,可得-
≤x≤-
,
∵x∈[-2π,2π],
∴函数的单调递增区间为:[-2π,-
]和[
,2π].
| 2π | ||
|
∵x∈[0,π],∴
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴sin(
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即函数在区间[0,π]上的值域为[-
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)原函数可化为y=-sin(
| 1 |
| 2 |
| π |
| 3 |
原函数的增区间即为y=sin(
| 1 |
| 2 |
| π |
| 3 |
令2kπ+
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得4kπ+
| 5π |
| 3 |
| 11π |
| 3 |
令k=0,可得
| 5π |
| 3 |
| 11π |
| 3 |
令k=-1,可得-
| 7π |
| 3 |
| π |
| 3 |
∵x∈[-2π,2π],
∴函数的单调递增区间为:[-2π,-
| π |
| 3 |
| 5π |
| 3 |
点评:本题考查三角函数的单调性和值域,涉及周期性和复合函数的单调性,属基础题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°
如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°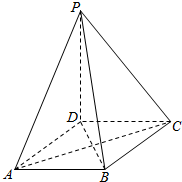 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.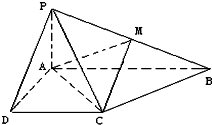 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=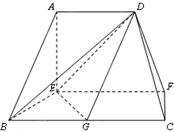 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.