题目内容
3.若函数f(x)=3x2-5x+a的两个零点分别为x1,x2.且有-2<x1<0与1<x2<3,试求出a的取值范围.分析 由条件利用二次函数的性质求得实数a的取值范围.
解答 解:∵f(x)=3x2-5x+a,
∴f(x)的图象是开口向上的抛物线.
由题意得:$\left\{\begin{array}{l}{f(-2)>0}\\{f(0)<0}\\{f(1)<0}\\{f(3)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{12+10+a>0}\\{a<0}\\{3-5+a<0}\\{23-15+a>0}\end{array}\right.$解的-8<a<0,
故a的取值范围为(-8,0).
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
11.下列各数中最小的数是( )
| A. | 111 111(2) | B. | 210(6) | C. | 1 000(4) | D. | 110(8) |
18.已知定义在R上的偶函数,f(x)在x≥0时,f(x)=ex+ln(x+1),若f(a)<f(a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,+∞) |
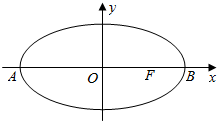 在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0. 长、宽、高分别为3,4,5的长方体,沿相邻面对角线截取一个三棱锥(如图),剩下几何体的体积为50.
长、宽、高分别为3,4,5的长方体,沿相邻面对角线截取一个三棱锥(如图),剩下几何体的体积为50.