题目内容
6.已知△ABC的三个顶点的坐标为A(0,1),B(1,0),C(0,-2),O为坐标原点,动点M满足|$\overrightarrow{CM}$|=1,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$|的最大值是( )| A. | $\sqrt{2}+1$ | B. | $\sqrt{7}+1$ | C. | $\sqrt{2}$-1 | D. | $\sqrt{7}$-1 |
分析 设点M的坐标是(x,y),由两点之间的距离公式化简|$\overrightarrow{CM}$|=1,判断出动点M的轨迹,由向量的坐标运算求出$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$,表示出|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$|并判断几何意义,转化为圆外一点与圆上点的距离最值问题,即可求出答案.
解答 解:设点M的坐标是(x,y),
∵C(0,-2),且|$\overrightarrow{CM}$|=1,
∴$\sqrt{{x}^{2}+(y+2)^{2}}=1$,则x2+(y+2)2=1,
即动点M的轨迹是以C为圆心、1为半径的圆,
∵A(0,1),B(1,0),
∴$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$=(x+1,y+1),
则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$|=$\sqrt{(x+1)^{2}+(y+1)^{2}}$,几何意义表示:
点M(x,y)与点A(-1,-1)之间的距离,即圆C上的点与点A(-1,-1)的距离,
∵点A(-1,-1)在圆C外部,
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$|的最大值是|AC|+1=$\sqrt{(0+1)^{2}+(-2+1)^{2}}$+1=$\sqrt{2}+1$,
故选A.
点评 本题考查向量的坐标运算、向量的模,动点的轨迹以及轨迹方程,两点之间的距离公式,以及圆外一点与圆上点的距离最值问题,考查转化思想.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| A. | 函数f(x)的图象关于点($\frac{π}{6}$,0)对称 | B. | 函数f(x)的图象关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
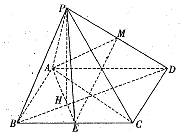 四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.