题目内容

3．若复数z满足z-1=$\frac{（i-1）^{2}+2}{1+i}$（i为虚数单位），则z在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、几何意义即可得出．

解答 解：z-1=$\frac{（i-1）^{2}+2}{1+i}$=$\frac{-2i+2}{1+i}$=$\frac{2（1-i）^{2}}{（1+i）（1-i）}$=-2i，
∴z=1-2i，
则z在复平面内对应的点（1，-2）位于第四象限．　
故选：D．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
13．李冶（1192-1279），真定栾城（今属河北石家庄市）人，金元时期的数学家、诗人、晚年在封龙山隐居讲学，数学著作多部，其中《益古演段》主要研究平面图形问题：求圆的直径，正方形的边长等，其中一问：现有正方形方田一块，内部有一个圆形水池，其中水池的边缘与方田四边之间的面积为13.75亩，若方田的四边到水池的最近距离均为二十步，则圆池直径和方田的边长分别是（注：240平方步为1亩，圆周率按3近似计算）（　　）
A．10步、50步B．20步、60步C．30步、70步D．40步、80步
14．在复平面中，复数$\frac{1}{（1+i）^{2}+1}$+i4对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
11．已知正项等差数列{an}中，a1+a2+a3=15，若a1+2，a2+5，a3+13成等比数列，则a10=（　　）
A．21B．22C．23D．24
18．已知正项等比数列{an}的第四项，第五项，第六项分别为1，m，9，则双曲线$C：\frac{y^2}{6}-\frac{x^2}{m}=1$的离心率为$\frac{\sqrt{6}}{2}$．
8．已知实数x、y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-a≥0}\\{2x-y-4≤0}\end{array}\right.$，若z=$\frac{y+1}{x+1}$的最小值为-$\frac{1}{4}$，则正数a的值为（　　）
A．$\frac{7}{6}$B．1C．$\frac{3}{4}$D．$\frac{8}{9}$
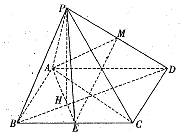15．四棱锥P-ABCD中，底面ABCD为矩形，$AB=2，BC=2\sqrt{2}，E$为BC的中点，连接AE，BD，交点H，PH⊥平面ABCD，M为PD的中点．
（1）求证：平面MAE⊥平面PBD；
（2）设PE=1，求二面角M-AE-C的余弦值．
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与抛物线y2=8x有一个共同的焦点F，两曲线的一个交点P，若|PF|=5，则点F到双曲线的渐近线的距离为$\sqrt{3}$．
13．下列函数中，既是偶函数又存在零点的是（　　）
A．y=x2+1B．y=|lgx|C．y=cosxD．y=ex-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网