题目内容
14.已知F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,A、B分别为椭圆C的左、上顶点,若BF的垂直平分线恰好过点A,则椭圆C的离心率为$\frac{\sqrt{3}-1}{2}$.分析 利用线段垂直平分线的性质可得线段BF的垂直平分线的方程,进而得出.
解答 解:由已知可得:A(-a,0),B(0,b),F(c,0),
线段BF的中点M$(\frac{c}{2},\frac{b}{2})$,kBF=$-\frac{b}{c}$,可得线段BF的垂直平分线的斜率为$\frac{c}{b}$.
∴线段BF的垂直平分线的方程为:y-$\frac{b}{2}$=$\frac{c}{b}$$(x-\frac{c}{2})$,
∵BF的垂直平分线恰好过点A,
∴0-$\frac{b}{2}$=$\frac{c}{b}$$(-a-\frac{c}{2})$,
化为:2e2+2e-1=0,
解得e=$\frac{\sqrt{3}-1}{2}$.
故答案为:$\frac{\sqrt{3}-1}{2}$.
点评 本题考查了椭圆的标准方程及其性质、线段垂直平分线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.已知α是第四象限角tanα=-$\frac{5}{12}$,则cosα=( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
3.设f(x)可导,F(x)=f(x)(1+|sinx|),则f(0)=0是F(x)在x=0处可导的( )
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
4.执行如图所示的程序框图.若输出的S=$\frac{1023}{512}$,则判断框内的条件可以为( )


| A. | i<10? | B. | i≤10? | C. | i<11? | D. | i≤11? |
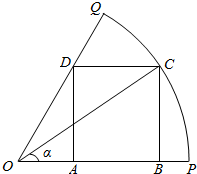 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,