题目内容
设函数f（x）=x2+bx+c，且f（-1）=f（3），则（ ）
| A、f（-1）＜c＜f（1） |
| B、c＜f（-1）＜f（1） |
| C、f（1）＜f（-1）＜c |
| D、f（1）＜c＜f（-1） |
考点：二次函数的性质
专题：函数的性质及应用
分析：先根据题意f（-1）=f（3）求出函数的解析式为f（x）=x2-2x+c，进而求出f（1），c，f（-1），即可比较大小得到答案．
解答：
解：由题意可得：二次函数f（x）=x2+bx+c且f（-1）=f（3），
所以1-b+c=9+3b+c，即b=-2，
所以f（x）=x2-2x+c．
所以f（1）=c-1，f（-1）=3+c，
所以f（1）＜c＜f（-1）．
故选：D．
所以1-b+c=9+3b+c，即b=-2，
所以f（x）=x2-2x+c．
所以f（1）=c-1，f（-1）=3+c，
所以f（1）＜c＜f（-1）．
故选：D．
点评：解决问题的关键是利用待定系数发求出函数的解析式，进而求出函数值进行比较大小．
练习册系列答案
相关题目
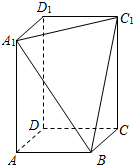在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，且这个几何体的体积为10．