题目内容
已知无穷数列{an}的各项均为正整数,Sn为数列{an}的前n项和.
(Ⅰ)若数列{an}是等差数列,且对任意正整数n都有Sn2=(Sn)2成立,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求数列{an}的通项公式.
(Ⅰ)若数列{an}是等差数列,且对任意正整数n都有Sn2=(Sn)2成立,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求数列{an}的通项公式.
考点:数列与函数的综合
专题:综合题,点列、递归数列与数学归纳法
分析:(1)设公差为d,则有Sn=na1+
d=n[
n+(a1-
)],由已知可得[
n2+(a1-
)]=[
n+(a1-
)]2,即可解得数列{an}的通项公式;
(2)(i)记An={1,2,…Sn},显然a1=S1=1,对于S2=a1+a2=1+a2,有A2={1,2,…S2}={1,a2,1+a2,|1-a2|}={1,2,3,4},即可解得a2的值.
(ii)由题意可知,Sn+1=Sn+(2Sn+1)=3Sn+1,又Sn+1+
=3(Sn+
),可得Sn=(S1+
)•3n-1-
=
•3n-
,即可求得an=Sn-Sn-1=3n-1.
| n(n+1) |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
(2)(i)记An={1,2,…Sn},显然a1=S1=1,对于S2=a1+a2=1+a2,有A2={1,2,…S2}={1,a2,1+a2,|1-a2|}={1,2,3,4},即可解得a2的值.
(ii)由题意可知,Sn+1=Sn+(2Sn+1)=3Sn+1,又Sn+1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(16分)
解:(1)设无穷等差数列{an}的公差为d,
则:Sn=na1+
d=n[
n+(a1-
)],
所以:Sn2=n2[
n2+(a1-
)]又(Sn)2=n2[
n+(a1-
)]2,
则:[
n2+(a1-
)]=[
n+(a1-
)]2,
所以:
则an=1或an=2n-1,
(2)(i)记An={1,2,…Sn},显然a1=S1=1,
对于S2=a1+a2=1+a2,
有A2={1,2,…S2}={1,a2,1+a2,|1-a2|}={1,2,3,4},
故1+a2=4,所以a2=3,
(ii)由题意可知,集合{a1,a2,…an}按上述规则,共产生Sn个正整数.而集合{a1,a2,…an,an+1}按上述规则产生的Sn+1个正整数中,除1,2,…Sn这Sn个正整数外,
还有an+1,an+1+i,|an+1-i|(i=1,2,…Sn),共2Sn+1个数.所以,Sn+1=Sn+(2Sn+1)=3Sn+1,
又Sn+1+
=3(Sn+
),
所以Sn=(S1+
)•3n-1-
=
•3n-
,
当n≥2时,an=Sn-Sn-1=
•3n-
-(
•3n-1-
)=3n-1而a1=1也满足an=3n-1.
所以,数列{an}的通项公式是an=3n-1.
解:(1)设无穷等差数列{an}的公差为d,
则:Sn=na1+
| n(n+1) |
| 2 |
| d |
| 2 |
| d |
| 2 |
所以:Sn2=n2[
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
则:[
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
| d |
| 2 |
所以:
|
(2)(i)记An={1,2,…Sn},显然a1=S1=1,
对于S2=a1+a2=1+a2,
有A2={1,2,…S2}={1,a2,1+a2,|1-a2|}={1,2,3,4},
故1+a2=4,所以a2=3,
(ii)由题意可知,集合{a1,a2,…an}按上述规则,共产生Sn个正整数.而集合{a1,a2,…an,an+1}按上述规则产生的Sn+1个正整数中,除1,2,…Sn这Sn个正整数外,
还有an+1,an+1+i,|an+1-i|(i=1,2,…Sn),共2Sn+1个数.所以,Sn+1=Sn+(2Sn+1)=3Sn+1,
又Sn+1+
| 1 |
| 2 |
| 1 |
| 2 |
所以Sn=(S1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,数列{an}的通项公式是an=3n-1.
点评:本题主要考查了等差数列通项公式的求法,考查了数列与函数的综合应用,考查计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
已知复数z=(1-sinθ)+icosθ(θ∈[
,π]),则|z|等于( )
| π |
| 2 |
A、cos
| ||||||
B、sin
| ||||||
C、
| ||||||
D、
|
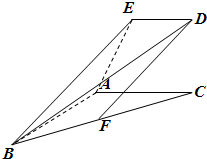 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.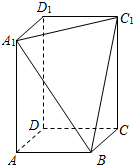 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.