题目内容
1.如图四面体O-ABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$ $\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,D为AB的中点,M为CD的中点,则$\overrightarrow{CM}$=$\frac{1}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$($\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$用表示)分析 由于$\overrightarrow{CM}$=$\frac{1}{2}\overrightarrow{CD}$,$\overrightarrow{CD}$=$\overrightarrow{OD}-\overrightarrow{OC}$,$\overrightarrow{OD}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,代入化简即可得出.
解答 解:$\overrightarrow{CM}$=$\frac{1}{2}\overrightarrow{CD}$,$\overrightarrow{CD}$=$\overrightarrow{OD}-\overrightarrow{OC}$,$\overrightarrow{OD}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,
∴$\overrightarrow{CM}$=$\frac{1}{2}×\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$-$\frac{1}{2}\overrightarrow{OC}$
=$\frac{1}{4}\overrightarrow{OA}+\frac{1}{4}$$\overrightarrow{OB}$-$\frac{1}{2}\overrightarrow{OC}$
=$\frac{1}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$.
故答案为:$\frac{1}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$.
点评 本题考查了向量的三角形法则与平行四边形法则,考查了推理能力与计算能力,属于中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | -9或1 | B. | 9或-1 | C. | 5或-5 | D. | 2或3 |
 我市三所重点中学进行高二期末联考,共有6000名学生参加,为了了解数学学科的学习情况,现从中随机抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
我市三所重点中学进行高二期末联考,共有6000名学生参加,为了了解数学学科的学习情况,现从中随机抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [80,90) | ① | ② |
| [90,100) | 0.050 | |
| [100,110) | 0.200 | |
| [110,120) | 36 | 0.300 |
| [120,130) | 0.275 | |
| [130,140) | 12 | ③ |
| [140,150) | 0.50 | |
| 合计 | ④ |
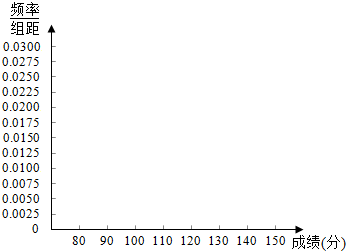
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体:①120分及以上的学生人数;②成绩在[127,150]中的概率.
| A. | 16 | B. | 64 | C. | 16或64 | D. | 以上都不对 |
| A. | a=6,b=4 | B. | a=-6,b=-4 | C. | a=-6,b=4 | D. | a=6,b=-4 |
| A. | (1-b,1-a) | B. | (1-a,1-b) | C. | (-a,-b) | D. | (-b,-a) |