题目内容
设f(x)=|x-1|+|x+1|,求f(x)≤x+2的解集.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:把要求得不等式去掉绝对值,化为与之等价的3个不等式组,求得每个不等式组的解集,再取并集,即得所求.
解答:
解:∵f(x)=|x-1|+|x+1|=
,
故f(x)≤x+2 即
①,或
②或
③,
解①求得1<x≤2;解②求得0≤x≤1;解③求得 x∈∅.
综上可得,不等式的解集为[0,2].
|
故f(x)≤x+2 即
|
|
|
解①求得1<x≤2;解②求得0≤x≤1;解③求得 x∈∅.
综上可得,不等式的解集为[0,2].
点评:本题主要考查绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解.体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
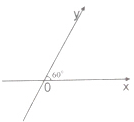 如图所示,∠xoy=60°,
如图所示,∠xoy=60°,| e1 |
| e2 |
| m |
| e1 |
| e2 |
| m |
| a |
| a |
| A、1 | ||||
B、
| ||||
C、C
| ||||
D、
|
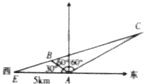 如图,某海岛观察哨A测得在海岛北偏东60°的C处有一轮船,80分钟后测得船在海岛北偏西60°的B处,又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口,如果轮船始终作匀速直线运动,问船速多少?
如图,某海岛观察哨A测得在海岛北偏东60°的C处有一轮船,80分钟后测得船在海岛北偏西60°的B处,又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口,如果轮船始终作匀速直线运动,问船速多少?已知函数f(x)=-x2+x,则f(x)从-1到-0.9的平均变化率为( )
| A、3 | B、0.29 |
| C、2.09 | D、2.9 |