题目内容
计算定积分：∫
dx= ．
0 -3 |
| 9-x2 |
考点：定积分
专题：计算题,导数的概念及应用
分析：本题利用定积分的几何意义计算定积分，即求被积函数y=
与直线x=0，x=-3所围成的图形的面积即可．
| 9-x2 |
解答：
解：解：由定积分的几何意义知
∫
dx是由曲线y=
，直线x=0，x=-3围成的封闭图形的面积，
故∫
dx=
=
，
故答案为：
．
∫
0 -3 |
| 9-x2 |
| 9-x2 |
故∫
0 -3 |
| 9-x2 |
| π•32 |
| 4 |
| 9π |
| 4 |
故答案为：
| 9π |
| 4 |
点评：本小题主要考查定积分、定积分的几何意义、圆的面积等基础知识，考查考查数形结合思想．属于基础题．
练习册系列答案
相关题目
设函数y=（2a-1）x在R上是增函数，则有（ ）
A、a≥
| ||
B、a≤
| ||
C、a＞
| ||
D、a＜
|
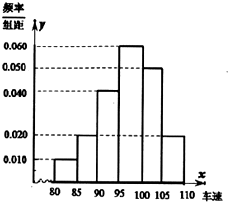2015年国庆节之前，市教育局为高三学生在紧张学习之余，不忘体能素质的提升，要求该市高三全体学生进行一套满分为120分的体能测试，市教育局为了迅速了解学生体能素质状况，按照全市高三测试学生的先后顺序，每间隔50人就抽取一人的抽样方法抽取40分进行统计分析，将这40人的体能测试成绩分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后，得到如图的频率分布直方图．曲线y=ln（2x+1）在点（0，0）处的切线方程为（ ）
| A、y=x | ||
| B、y=2x | ||
C、y=
| ||
| D、y=ln2•x |
已知函数f（x）=x3-log2（
-x），则对于任意实数a、b（a+b≠0），
的值（ ）
| x2+1 |
| f(a)+f(b) |
| a3+b3 |
| A、恒大于0 | B、恒小于1 |
| C、恒大于-1 | D、不确定 |