题目内容
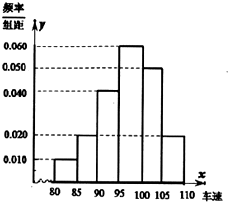 2015年国庆节之前,市教育局为高三学生在紧张学习之余,不忘体能素质的提升,要求该市高三全体学生进行一套满分为120分的体能测试,市教育局为了迅速了解学生体能素质状况,按照全市高三测试学生的先后顺序,每间隔50人就抽取一人的抽样方法抽取40分进行统计分析,将这40人的体能测试成绩分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后,得到如图的频率分布直方图.
2015年国庆节之前,市教育局为高三学生在紧张学习之余,不忘体能素质的提升,要求该市高三全体学生进行一套满分为120分的体能测试,市教育局为了迅速了解学生体能素质状况,按照全市高三测试学生的先后顺序,每间隔50人就抽取一人的抽样方法抽取40分进行统计分析,将这40人的体能测试成绩分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后,得到如图的频率分布直方图.(1)市教育局在采样中,用的是什么抽样方法?并估计这40人体能测试成绩平均数;
(2)从体能测试成绩在[80,90)的学生中任抽取2人,求抽出的2人体能测试成绩在[85,90)概率.
参考数据:82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02=19.4.
考点:频率分布直方图
专题:概率与统计
分析:(1)根据“每间隔50人就抽取一人”,是系统抽样原理,从而得出抽样的方法;根据频率分布直方图计算测试成绩的平均数;
(2)从频率分布直方图得出,计算体能测试成绩在[80,85)与[85,90)的人数,求出对应的概率是多少.
(2)从频率分布直方图得出,计算体能测试成绩在[80,85)与[85,90)的人数,求出对应的概率是多少.
解答:
解:(1)根据“每间隔50人就抽取一人”,符合系统抽样的原理,
∴市教育局在采样中,用到的是系统抽样方法;…(3分)
估计这40人体能测试成绩平均数为:
(82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02)×5=19.4×5=97;.6分
(2)从图中可知,体能测试成绩在[80,85)的人数为m1=0.01×5×40=2(人),分别记为B1、B2;
体能测试成绩在[85,90)的人数是=0.02×5×40=(人),分别记为A1、A2、A3、A4;
从中任抽取2人,共有B1B2、B1A1、B1A2、B1A3、B1A4、B2A1、B2A2、B2A3、B2A4、
A1A2、A1A3、A1A4、A2A3、A2A4、A3A4,15种,
体能测试成绩在[85,90)的抽取方法有A1A2、A1A3、A1A4、A2A3、A2A4、A3A4,6种,
∴体能测试成绩在[85,90)的概率为P=
=0.4.
∴市教育局在采样中,用到的是系统抽样方法;…(3分)
估计这40人体能测试成绩平均数为:
(82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02)×5=19.4×5=97;.6分
(2)从图中可知,体能测试成绩在[80,85)的人数为m1=0.01×5×40=2(人),分别记为B1、B2;
体能测试成绩在[85,90)的人数是=0.02×5×40=(人),分别记为A1、A2、A3、A4;
从中任抽取2人,共有B1B2、B1A1、B1A2、B1A3、B1A4、B2A1、B2A2、B2A3、B2A4、
A1A2、A1A3、A1A4、A2A3、A2A4、A3A4,15种,
体能测试成绩在[85,90)的抽取方法有A1A2、A1A3、A1A4、A2A3、A2A4、A3A4,6种,
∴体能测试成绩在[85,90)的概率为P=
| 6 |
| 15 |
点评:本题考查了频率分布直方图的应用问题,解题时应根据抽样方法的特征进行判断,根据频率分布直方图进行计算,是基础题.

练习册系列答案
相关题目
若函数f(x)的唯一一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,则下列结论中正确的是( )
| A、f(x)在区间(0,1)内一定有零点 |
| B、f(x)在区间[2,16)内没有零点 |
| C、f(x)在区间(0,1)或(1,2)内一定有零点 |
| D、f(x)在区间(1,16)内没有零点 |
如图所示的流程图,若输入的x=-5.5,则输出的结果为( )


| A、-2 | B、-1 | C、0 | D、1 |
函数y=x
的图象是图中的哪一个( )
| 2 |
| 3 |
A、 |
B、 |
C、 |
D、 |