题目内容
函数f(x)=sin(ωx+φ)cos(ωx+φ)(ω>0)的相邻的两个对称中心的距离为1,且能在x=2时取得最大值,则φ的一个值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:二倍角的正弦,正弦函数的图象
专题:三角函数的图像与性质
分析:先求得函数f(x)=
sin(2ωx+2φ),根据它的相邻的两个对称中心的距离为1求得ω,再根据x=2时取得最大值,求得φ的值.
| 1 |
| 2 |
解答:
解:∵函数f(x)=sin(ωx+φ)cos(ωx+φ)=
sin2(ωx+φ)=
sin(2ωx+2φ)
(ω>0)的相邻的两个对称中心的距离为1,
∴
•
=1,解得ω=
.
再根据x=2时取得最大值,可得2•
•2+2φ=2kπ+
,k∈z,
解得 φ=kπ-
,k∈z,
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
(ω>0)的相邻的两个对称中心的距离为1,
∴
| 1 |
| 2 |
| 2π |
| 2ω |
| π |
| 2 |
再根据x=2时取得最大值,可得2•
| π |
| 2 |
| π |
| 2 |
解得 φ=kπ-
| 3π |
| 4 |
故选:A.
点评:本题主要考查二倍角公式、正弦函数的对称性和最值,属于中档题.

练习册系列答案
相关题目
若向量
=(1,1-x),
=(1,1+x),则函数f(x)=
是( )
| a |
| b |
| ||||||
| 4-|x-4| |
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、减函数 |
下列各组命题:
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
)n,
,3n(n∈N*)成等比数列.
其中,p是q的充分不必要条件的是( )
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
| 1 |
| 3 |
| 3 |
| 3n |
其中,p是q的充分不必要条件的是( )
| A、(1)(2) |
| B、(1)(4) |
| C、(1)(3) |
| D、(2)(3)(4) |
从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x∈[1,10],执行如图所示的程序框图,则输出x的值不小于55的概率为( )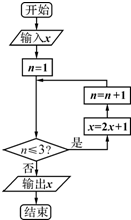

A、
| ||
B、
| ||
C、
| ||
D、
|
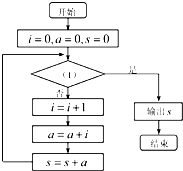 在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是
在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是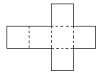 如图是一个正方体纸盒的展开图,把1、-1、2、-2、
如图是一个正方体纸盒的展开图,把1、-1、2、-2、