题目内容
设函数f(x)=1-|2x-1|,x∈[0,1].函数g(x)=f(f(x))-ax有4个零点.则实数a的取值范围是 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:将函数的零点问题转化为两个函数的交点问题,可通过分类讨论的方式求出函数f(f(x))的表达式,结合数形结合一目了然.
解答:
解:①当x∈[0,
]时,
f(x)=1+2x-1=2x,
∴f(f(x))=1-|4x-1|,
当x∈[0,
]时:
f(f(x))=4x,
当x∈[
,
]时:
f(f(x))=2-4x,
②当x∈[
,1]时,
f(x)=1-(2x-1)=2-2x,
∴f(f(x))=1-|3-4x|,
x∈[
,
]时:
f(f(x))=4-4x,
x∈[
,1]时:
f(f(x))=4x-2,
令h(x)=ax,
∴g(x)的零点个数等价于f(f(x))和g(x)的交点个数,
如图示:
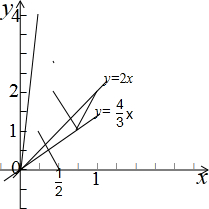 ,
,
∴
<a≤2,
故答案为:(
,2].
| 1 |
| 2 |
f(x)=1+2x-1=2x,
∴f(f(x))=1-|4x-1|,
当x∈[0,
| 1 |
| 4 |
f(f(x))=4x,
当x∈[
| 1 |
| 4 |
| 1 |
| 2 |
f(f(x))=2-4x,
②当x∈[
| 1 |
| 2 |
f(x)=1-(2x-1)=2-2x,
∴f(f(x))=1-|3-4x|,
x∈[
| 1 |
| 2 |
| 3 |
| 4 |
f(f(x))=4-4x,
x∈[
| 3 |
| 4 |
f(f(x))=4x-2,
令h(x)=ax,
∴g(x)的零点个数等价于f(f(x))和g(x)的交点个数,
如图示:
 ,
,∴
| 4 |
| 3 |
故答案为:(
| 4 |
| 3 |
点评:本题考察了函数的零点问题,渗透了分类讨论思想,数形结合思想,是一道中档题.

练习册系列答案
相关题目
已知i为虚数单位,则复数
的虚部为( )
| 25 |
| 3+4i |
A、
| ||
| B、4 | ||
| C、-4 | ||
| D、-4i |
已知双曲线
-
=1的离心率为e,焦点为F的抛物线y2=2px与直线y=k(x-
)交于A,B两点,且
=e,则k的值为( )
| x2 |
| 4 |
| y2 |
| 12 |
| p |
| 2 |
| 丨AF丨 |
| 丨BF丨 |
A、2
| ||
B、2
| ||
C、±2
| ||
D、±2
|
 已知质点P在半径为10cm的圆上按逆时针方向做匀速圆周运动,角速度是1rad/s,设A(10,0)为起始点,记点P在y轴上的射影为M,则10π秒时点M的速度是
已知质点P在半径为10cm的圆上按逆时针方向做匀速圆周运动,角速度是1rad/s,设A(10,0)为起始点,记点P在y轴上的射影为M,则10π秒时点M的速度是 如图表示甲、乙两名篮球运动员每场得分情况的茎叶图,则甲、乙得分的中位数分别是a,b,则a+b=
如图表示甲、乙两名篮球运动员每场得分情况的茎叶图,则甲、乙得分的中位数分别是a,b,则a+b=