题目内容
已知点M(-1,0),N(1,0),动点P(x,y)满足:|PM|•|PN|=
,
(1)求P的轨迹C的方程;
(2)是否存在过点N(1,0)的直线l与曲线C相 交于A、B两点,并且曲线C存在点Q,使四边形OAQB为平行四边形?若存在,求出平行四边形OAQB的面积;若不存在,说明理由.
| 4 |
| 1+cos∠MPN |
(1)求P的轨迹C的方程;
(2)是否存在过点N(1,0)的直线l与曲线C相 交于A、B两点,并且曲线C存在点Q,使四边形OAQB为平行四边形?若存在,求出平行四边形OAQB的面积;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(x,y),由已条条件推导出
•
=
,由此能求出P的轨迹C的方程.
(Ⅱ)设A(x1,y1)、B(x2,y2),设l:x=my+1,代入椭圆方程得(2m2+3)y2+4my-4=0,由此利用根的判别式和韦达定理结合已条件推导出存在满足条件的点P,使得四边形OAPB为平行四边形,且该平行四边形的面积为
.
| (x+1)2+y2 |
| (x-1)2+y2 |
| 4 | ||||||
1+
|
(Ⅱ)设A(x1,y1)、B(x2,y2),设l:x=my+1,代入椭圆方程得(2m2+3)y2+4my-4=0,由此利用根的判别式和韦达定理结合已条件推导出存在满足条件的点P,使得四边形OAPB为平行四边形,且该平行四边形的面积为
| 3 |
| 2 |
| 2 |
解答:
解:(1)设动点P(x,y),
∵点M(-1,0),N(1,0),动点P(x,y)满足:|PM|•|PN|=
,
∴
•
=
,
整理,得
+
=1,
∴P的轨迹C的方程为
+
=1.
(Ⅱ)设A(x1,y1)、B(x2,y2),
由题意知l的斜率一定不为0,∴设l:x=my+1,
代入椭圆方程整理得(2m2+3)y2+4my-4=0,
△=16m2+16(2m2+3)>0.
y1+y2=-
, y1y2=-
…①,
假设存在点Q,使得四边形OAQB为平行四边形,
其充要条件为
=
+
,
则点Q的坐标为(x1+x2,y1+y2).
由点Q在椭圆上,即
+
=1.
整理得2x12+3y12+2x22+3y22+4x1x2+6y1y2=6.
又A、B在椭圆上,即2x12+3y12=6, 2x22+3y22=6.
∴2x1x2+3y1y2=3…②
将x1x2=(my1+1)(my2+1)=m2y1y2+m(y1+y2)+1代入,
由①②解得m=±
.
当m=
时,解得y1=-
, y2=
.
从而x1=0, x2=
∴A(0,-
), B(
,
),
∴
=(0,-
),
=(
,
),
∴cos∠AOB=
=-
, sin∠AOB=
.S平行四边形OAQB=|
||
|sin∠AOB=
.
同理当m=-
时,S平行四边形OAQB=
.
综上,存在满足条件的点P,使得四边形OAPB为平行四边形,
且该平行四边形的面积为
.
∵点M(-1,0),N(1,0),动点P(x,y)满足:|PM|•|PN|=
| 4 |
| 1+cos∠MPN |
∴
| (x+1)2+y2 |
| (x-1)2+y2 |
| 4 | ||||||
1+
|
整理,得
| x2 |
| 3 |
| y2 |
| 2 |
∴P的轨迹C的方程为
| x2 |
| 3 |
| y2 |
| 2 |
(Ⅱ)设A(x1,y1)、B(x2,y2),
由题意知l的斜率一定不为0,∴设l:x=my+1,
代入椭圆方程整理得(2m2+3)y2+4my-4=0,
△=16m2+16(2m2+3)>0.
y1+y2=-
| 4m |
| 2m2+3 |
| 4 |
| 2m2+3 |
假设存在点Q,使得四边形OAQB为平行四边形,
其充要条件为
| OQ |
| OA |
| OB |
则点Q的坐标为(x1+x2,y1+y2).
由点Q在椭圆上,即
| (x1+x2)2 |
| 3 |
| (y1+y2)2 |
| 2 |
整理得2x12+3y12+2x22+3y22+4x1x2+6y1y2=6.
又A、B在椭圆上,即2x12+3y12=6, 2x22+3y22=6.
∴2x1x2+3y1y2=3…②
将x1x2=(my1+1)(my2+1)=m2y1y2+m(y1+y2)+1代入,
由①②解得m=±
| ||
| 2 |
当m=
| ||
| 2 |
| 2 |
| ||
| 2 |
从而x1=0, x2=
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
∴
| OA |
| 2 |
| OB |
| 3 |
| 2 |
| ||
| 2 |
∴cos∠AOB=
| ||||
|
|
|
| 3 | ||
|
| OA |
| OB |
| 3 |
| 2 |
| 2 |
同理当m=-
| ||
| 2 |
| 3 |
| 2 |
| 2 |
综上,存在满足条件的点P,使得四边形OAPB为平行四边形,
且该平行四边形的面积为
| 3 |
| 2 |
| 2 |
点评:本题考查点的轨迹方程的求法,考查满足条件的点是否存在的判断,考查平行四边形面积的求法,综合性强,难度大,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
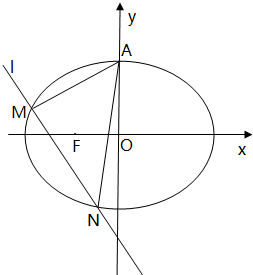 已知椭圆C:
已知椭圆C: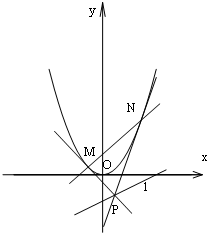 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.