题目内容
设函数f(x)=x2-mlnx,g(x)=x2-x+a.
(1) 当a=0时,f(x)≥g(x)在(1,+∞),上恒成立,求实数m的取值范围;
(2) 当m=2时,若函数h(x)=f(x)-g(x)在[1,3]上恰有两个不同的零点,求实数a的取值范围.
解:(1)由a=0,f(x)≥g(x)可得-mln x≥-x
x∈(1,+∞),即m≤ ,记φ(x)=
,记φ(x)= ,
,
则f(x)≥g(x)在(1,+∞)上恒成立等价于m ≤φ(x)min.
求得φ′(x)=
当x∈(1,e)时, φ′(x)<0;
当x∈(e,+∞)时, φ′(x)>0.
故φ(x)在x=e处取得极小值,也是最小值,即φ(x)min=φ(e)=e,故m≤e.
所以,实数m的取值范围为;(- ¥,e]
(2)函数h(x)=f(x)-g(x)在[1,3]上恰有两个不同的零点
等价于方程x-2ln x=a,在[1,3]上恰有两个相异实根.
令k(x)=x-2ln x,则k′(x)=1- .
.
当x∈[1,2)时,k′(x)<0;
当x∈(2,3]时,k′(x)>0,
∴k(x)在[1,2)上是单调递减函数,在(2,3]上是单调递增
函数.故k(x)min=k(2)=2-2ln 2,
又k(1)=1,k(3)=3-2ln 3,
∵k(1)>k(3),∴只需k(2)<a≤k(3),
故a的取值范围是(2-2ln 2,3-2ln 3].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :
: ,
, :
: ,若
,若 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是 .
的取值范围是 .  恒成立,则
恒成立,则 的范围是____________.
的范围是____________. 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 ,有
,有 ,则
,则 的最小值为 ( )
的最小值为 ( ) B.
B. C.
C. D.
D.

 ,若
,若 ,则
,则 .
. a2 B.2
a2 B.2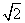 a2 C.
a2 C. a2 D.
a2 D. a2
a2 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( ) B.
B. C.
C. D.
D.
 ,则输出的结果是( )
,则输出的结果是( )