题目内容

用符号“?”与“?”表示下列含有量词的命题：
（1）自然数的平方大于零；
（2）圆x2+y2=r2上任一点到圆心的距离是r；
（3）存在一对整数x，y，使得2x+4y=3；
（4）存在一个无理数，它的立方是有理数．
考点：全称命题,特称命题
专题：简易逻辑
分析：根据全称，特称命题的表达方式书写．
解答： 解：（1）?x∈N，则x2＞0；
（2）圆x2+y2=r2的圆心为O，?点P在圆上，则|OP|=r；
（3）?一对整数x，y，使得2x+4y=3；
（4）?x∈C
 
Q
R
，则x3是有理数．
点评：本题考查了全称，特称命题的符号语言的书写，难度不大．
练习册系列答案
相关题目
求曲线
x=
2
3
(t+
1
t
)
y=
3
4
(t-
1
t
)
 的离心率．
已知角α的终边上一点坐标为P（-3t，4t）（t≠0），求2sinα+cosα的值．
已知函数f（x）=
a
x
+lnx，g（x）=
1
2
bx2-2x+2，a，b∈R．
（Ⅰ）记函数h（x）=f（x）+g（x），当a=0，h（x）在（0，1）上有且只有一个极值点，求实数b的取值范围；
（Ⅱ）记函数F（x）=|f（x）|，若存在一条过原点的直线l与y=F（x）的图象有两个切点，求a的取值范围，并证明你的结论．
已知函数f（x）=log2（k•2x+1-2），k∈R．
（1）当k=1时，求函数f（x）的定义域；
（2）当k=3是，求函数f（x）的零点；
（3）若函数f（x）在区间[0，10]上总有意义，求k的取值范围．
求下列函数的定义域和值域；
（1）y=
1
1+tanx
；
（2）y=lgtanx+
16-x2
．
已知函数f（x）=
x2+a
x+b
，（a，b∈R），若f（x）为奇函数，且f（1）=5．
（1）求函数f（x）的解析式；
（2）用定义判断f（x）在（0，+∞）上的单调性，并写出相应的单调区间．
设f（x）=
sin
π
3
x，		x≤2011
f(x-4)，x＞2011
，则f（2012）=（　　）
A、
1
2
B、-
1
2
C、
3
2
D、-
3
2
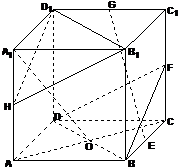正方体ABCD-A1B1C1D1中，F，H分别为棱CC1，AA1的中点，O为AC与BD的交点．
（1）平面BDF∥平面B1D1H；
（2）A1O⊥平面BDF；
（3）平面A1BD⊥平面BDF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网