题目内容
已知函数f(x)=
,(a,b∈R),若f(x)为奇函数,且f(1)=5.
(1)求函数f(x)的解析式;
(2)用定义判断f(x)在(0,+∞)上的单调性,并写出相应的单调区间.
| x2+a |
| x+b |
(1)求函数f(x)的解析式;
(2)用定义判断f(x)在(0,+∞)上的单调性,并写出相应的单调区间.
考点:函数解析式的求解及常用方法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)
=-
,得出b=0,f(1)=5得出a=4,
(2)设变量,作差分解因式f(x1)-f(x2)=(x1-x2)
可判断单调性.
| x2+a |
| -x+b |
| x2+a |
| x+b |
(2)设变量,作差分解因式f(x1)-f(x2)=(x1-x2)
| x1x2-4 |
| x1x2 |
解答:
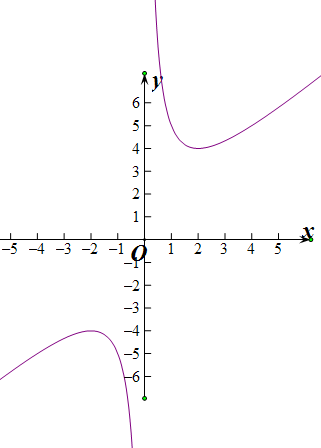 (1)解:∵函数f(x)=
(1)解:∵函数f(x)=
,(a,b∈R),若f(x)为奇函数,
∴f(-x)=-f(x),
即
=-
,
b=0,
∵f(1)=5.
∴a=4,
∴f(x)=x+
,
(2)f(x)=x+
的函数图象,(0,2)(-2,0)上单调递减,(2,+∞)(-∞,-2)上单调递增,
证明:∵设0<x1<x2<2,0<x1x2<4
f(x1)-f(x2)=(x1-x2)
>0,
∴f(x1)>f(x2),
∴在(0,2)上单调递减,
∵设2<x1<x2,x1x2>4,x1x2-4>0,
f(x1)-f(x2)=(x1-x2)
<0
∴f(x1)<f(x2),
∴在(2,+∞)上单调递增,
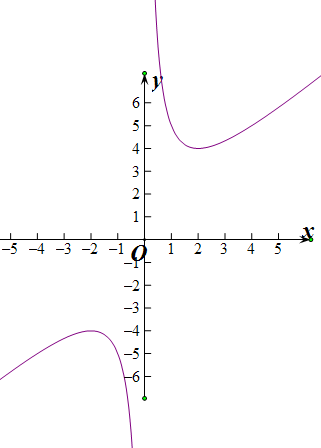 (1)解:∵函数f(x)=
(1)解:∵函数f(x)=| x2+a |
| x+b |
∴f(-x)=-f(x),
即
| x2+a |
| -x+b |
| x2+a |
| x+b |
b=0,
∵f(1)=5.
∴a=4,
∴f(x)=x+
| 4 |
| x |
(2)f(x)=x+
| 4 |
| x |
证明:∵设0<x1<x2<2,0<x1x2<4
f(x1)-f(x2)=(x1-x2)
| x1x2-4 |
| x1x2 |
∴f(x1)>f(x2),
∴在(0,2)上单调递减,
∵设2<x1<x2,x1x2>4,x1x2-4>0,
f(x1)-f(x2)=(x1-x2)
| x1x2-4 |
| x1x2 |
∴f(x1)<f(x2),
∴在(2,+∞)上单调递增,
点评:本题考查了函数的性质,单调性的判断,属于基础题,掌握好因式分解是关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
若非零向量
,
,满足|
|=|
|=|
-
|,则
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是减函数,设a=f(log4(
)),b=f(log2(
)),c=f(21.1),则a,b,c的大小关系是( )
| 1 |
| 7 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
已知函数f(x)=
,若对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是( )
| ex+m |
| ex+1 |
A、[
| ||
| B、[0,1] | ||
| C、[1,2] | ||
D、[
|