题目内容
1．已知两条直线方程：l1：ax-y+6=0，l2：x+ay-4=0（1）求证：l1与l2的交点总在同一个圆C上．
（2）求证：无论a取何值，直线l：（a+1）x-（2a-1）y+6a-9=0恒过定点．
分析 （1）联立$\left\{\begin{array}{l}{ax-y+6=0}\\{x+ay-4=0}\end{array}\right.$，消去a，得x2+y2-4x-6y=0，由此能证明l1与l2的交点总在同一个圆C上．
（2）要证明直线过定点的问题，我们可将已知直线的方程化为关于a的一次方程的形式，然后根据方程等0恒成立，则所有系数均为0，求出定点值．
解答 证明：（1）∵两条直线方程：l1：ax-y+6=0，l2：x+ay-4=0，
∴$\left\{\begin{array}{l}{ax-y+6=0}\\{x+ay-4=0}\end{array}\right.$，消去a，得x2+y2-4x-6y=0，
它是以（2，3）为圆心，以r=$\frac{1}{2}\sqrt{16+36}$=$\sqrt{13}$为半径的圆，
∴l1与l2的交点总在同一个圆C上．
（2）∵直线l：（a+1）x-（2a-1）y+6a-9=0，
∴（x-2y+6）a+（x+y-9）=0，
∵直线l：（a+1）x-（2a-1）y+6a-9=0过定点，
∴$\left\{\begin{array}{l}{x-2y+6=0}\\{x+y-9=0}\end{array}\right.$，解得x=4，y=5．
∴无论a取何值，直线l：（a+1）x-（2a-1）y+6a-9=0过定点（4，5）．
点评 要求直线过定点的问题，我们可将已知直线的方程化为关于a的一次方程的形式，然后根据方程等0恒成立，则所有系数均为0，构造方程组求解．
练习册系列答案
考前必练系列答案
相关题目
2．1+4+7+10+…+（3n+1）等于（ ）
| A． | $\frac{n（3n+8）}{2}$ | B． | $\frac{（n+2）（3n+8）}{2}$ | C． | $\frac{（n+1）（3n+2）}{2}$ | D． | $\frac{n（3n-1）}{2}$ |
3．函数y=cosx的定义域为[a，b]，值域为[-1，$\frac{1}{2}$]，则b-a的最大值是（ ）
| A． | π | B． | $\frac{4π}{3}$ | C． | $\frac{5π}{3}$ | D． | 2π |
20．函数y=cos（$\frac{π}{2}$-x）sin（$\frac{π}{2}$+x）的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |
6．下列命题中的真命题是（ ）
| A． | ?x0∈R，使得x0+$\frac{1}{x0}$=$\frac{3}{2}$ | B． | ?x∈（0，+∞），ex＞x+1 | ||
| C． | ?x0∈R，使得x${\;}_{{0}^{\;}}$2-x0+1=0 | D． | ?x∈（0，π），sinx＞cosx |
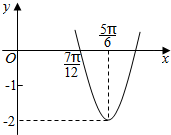函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）在区间[0，$\frac{π}{2}$]上的最小值为-1．