题目内容
13.若关于x的方程4x+2x+m-2=0有实数根,求实数m的取值范围.分析 m=-4x-2x+2,使用换元法求出右侧函数的值域即为m的取值范围.
解答 解:∵4x+2x+m-2=0,∴m=-4x-2x+2.令t=2x,f(t)=-t2-2t+2,则t>0,
∵f(t)的对称轴为t=-1,∴f(t)在(0,+∞)上单调递减.∴f(t)<f(0)=2.
∵方程4x+2x+m-2=0有实数根,∴m<2.
∴m的取值范围是(-∞,2).
点评 本题考查了根的存在性判断,函数的值域及换元思想,属于中档题.

练习册系列答案
相关题目
14.若函数y=(a2-1)x在R上是减函数,则有( )
| A. | |a|<1 | B. | 1<|a|<2 | C. | 1<|a|<$\sqrt{2}$ | D. | |a|>$\sqrt{2}$ |
1.已知两条直线方程:l1:ax-y+6=0,l2:x+ay-4=0
(1)求证:l1与l2的交点总在同一个圆C上.
(2)求证:无论a取何值,直线l:(a+1)x-(2a-1)y+6a-9=0恒过定点.
(1)求证:l1与l2的交点总在同一个圆C上.
(2)求证:无论a取何值,直线l:(a+1)x-(2a-1)y+6a-9=0恒过定点.
18.若直线ax+by=2与圆x2+y2=1有公共点,则( )
| A. | a2+b2≤4 | B. | a2+b2≥4 | C. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≤4 | D. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥4 |
5.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -3 | B. | -5 | C. | -6 | D. | -14 |
2.下列各数中最大的数为( )
| A. | 101111(2) | B. | 1210(3) | C. | 112(8) | D. | 69(12) |
3.下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是( )
| A. | y=2x | B. | y=$\sqrt{x}$ | C. | y=|x| | D. | y=-x2+1 |
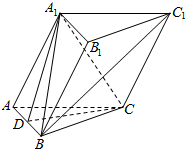 在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.