题目内容
7.已知数列{an}是公比为2的等比数列,且a2,a3+1,a4成等差数列.(1)求数列{an}的前n项和Sn
(2)设bn=$\frac{2n(n-1){a}_{n}}{{3}^{n}}$(n∈N*),求当bn取得最大值时正整数n的值.
分析 (1)数列{an}是公比为2的等比数列,且a2,a3+1,a4成等差数列.可得2(a3+1)=a2+a4,解得a1,即可得出.
(2)由(1)可得:an.bn=$n(n-1)•(\frac{2}{3})^{n}$,n≥2时,$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{2(n+1)}{3(n-1)}$,对n分类讨论,即可比较出大小关系.
解答 解:(1)数列{an}是公比为2的等比数列,且a2,a3+1,a4成等差数列.
∴2(a3+1)=a2+a4,
∴2(4a1+1)=2a1+8a1,解得a1=1.
∴数列{an}的前n项和Sn=$\frac{{2}^{n}-1}{2-1}$=2n-1.
(2)由(1)可得:an=2n-1.
bn=$\frac{2n(n-1){a}_{n}}{{3}^{n}}$=$n(n-1)•(\frac{2}{3})^{n}$,
n≥2时,$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{n(n+1)•(\frac{2}{3})^{n+1}}{n(n-1)•(\frac{2}{3})^{n}}$=$\frac{2(n+1)}{3(n-1)}$,
b1=0,b2=$\frac{8}{9}$,
当2≤n≤4时,$\frac{{b}_{n+1}}{{b}_{n}}$>1;当n=5时,b6=b5;
当n≥6时,$\frac{{b}_{n+1}}{{b}_{n}}$<1.
∴当n=5时,bn取得最大值,b6=b5=1.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
17.已知数列{an}满足:a1=2,an+1=-2an(n∈N*).若从数列{an}的前10项中随机抽取一项,则该项不小于8的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
2.下列函数中,既是偶函数又在区间(0,+∞)内是单调减函数的是( )
| A. | y=log0.5|x| | B. | y=${3}^{{x}^{2}}$ | C. | y=-x2+x | D. | y=cosx |
1.已知两条直线方程:l1:ax-y+6=0,l2:x+ay-4=0
(1)求证:l1与l2的交点总在同一个圆C上.
(2)求证:无论a取何值,直线l:(a+1)x-(2a-1)y+6a-9=0恒过定点.
(1)求证:l1与l2的交点总在同一个圆C上.
(2)求证:无论a取何值,直线l:(a+1)x-(2a-1)y+6a-9=0恒过定点.
5.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -3 | B. | -5 | C. | -6 | D. | -14 |
6.某四棱锥的三视图如图所示,则该四棱锥的侧面积是( )
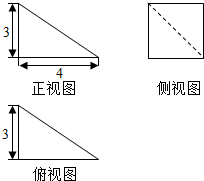

| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
 已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.
已知函数f(x)为定义在[-2,2]上的图象,如图所示,请分别画出下列函数的图象.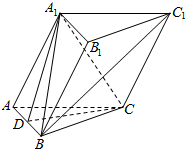 在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.