题目内容
13.下列四种说法中,错误的个数是( )①命题“若函数f(x)=sinx+cosx,则$f'(\frac{π}{4})=0$”是真命题;
②“若am2<bm2,则a<b”的逆命题为真;
③“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;
④命题“?x∈R,均有x2-3x-2≥0”的否定是:“?x0∈R,使得x02-3x0-2≤0”
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①,由f′(x)=-sinx+cosx,得$f'(\frac{π}{4})=0$;
②,由m2≤0可判定;
③,若p∨q为真时,p∧q不一定为真,p∧q为真时,p∨q一定为真;
④,“≥0”的否定是:“<”;
解答 解:对于①,∵f′(x)=-sinx+cosx,则$f'(\frac{π}{4})=0$”,故正确;
对于②,∵a<b不能推出am2<bm2,故错;
对于③,若p∨q为真时,p∧q不一定为真,p∧q为真时,p∨q一定为真,故正确;
对于④,命题“?x∈R,均有x2-3x-2≥0”的否定是:“?x0∈R,使得x02-3x0-2<0”,故错;
故答案为:C
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知集合A={x|log2(x+1)>0},B={x|0<x<1},则∁AB=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
4.数列-1,3,-5,7,-9,…的一个通项公式为( )
| A. | an=2n-1 | B. | an=(-1)n(1-2n) | C. | an=(-1)n(2n-1) | D. | an(-1)n+1(2n-1) |
8.某四棱锥的三视图如图所示,则俯视图的面积为( )
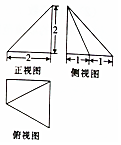

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
5.幂函数f(x)=(m2-2m+1)x2m-1在(0,+∞)上为增函数,则实数m的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 1或2 |
2.某企业第三年的产量比第一年的产量增加44%,若每年的平均增长率相同(设为x),则以下结论正确的是( )
| A. | x>22% | B. | x<22% | C. | x=22% | D. | 以上都不对 |
12.已知向量|$\overrightarrow{a}$|=3,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$,则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |