题目内容
12.已知向量|$\overrightarrow{a}$|=3,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$,则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
分析 对|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$两边平方计算|$\overrightarrow{b}$|,根据向量的数量积的定义计算向量的夹角的余弦值,再代入投影公式计算.
解答 解:∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$,∴|$\overrightarrow{a}$|2+2$\overrightarrow{a}•\overrightarrow{b}$+|$\overrightarrow{b}$|2=$\frac{27}{2}$,
即9+3+|$\overrightarrow{b}$|2=$\frac{27}{2}$,∴|$\overrightarrow{b}$|=$\frac{\sqrt{6}}{2}$,
设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,则$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ,
即$\frac{3}{2}$=3×$\frac{\sqrt{6}}{2}$cosθ,∴cosθ=$\frac{\sqrt{6}}{6}$.
∴向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$|cosθ=3×$\frac{\sqrt{6}}{6}$=$\frac{\sqrt{6}}{2}$.
故选:B.
点评 本题考查了平面向量的数量积运算,属于基础题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
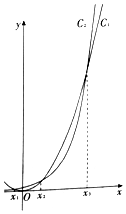 函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点.
函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点. 某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.
某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习. 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.