题目内容
12.已知m∈R,命题p:对任意实数x,不等式x2-2x-1≥m2-3m恒成立,若¬p为真命题,则m的取值范围是(-∞,1)∪(2,+∞).分析 由对任意x∈R,不等式x2-2x-1≥m2-3m恒成立,运用二次函数的最值求法,可得m2-3m≤-2,解不等式可得m的范围,再由¬p为真命题时,则P为假命题,即可得到所求m的范围.
解答 解:∵对任意x∈R,不等式x2-2x-1≥m2-3m恒成立,
∴${[{{{({x-1})}^2}-2}]_{min}}≥{m^2}-3m$,即m2-3m≤-2,
即有(m-1)(m-2)≤0,
解得1≤m≤2.
因此,若¬p为真命题时,则P为假命题,
可得m的取值范围是(-∞,1)∪(2,+∞).
故答案为:(-∞,1)∪(2,+∞).
点评 本题考查不等式恒成立问题的解法,注意运用二次函数的最值求法和二次不等式的解法,同时考查命题的真假判断,考查转化和运算能力,属于中档题.

练习册系列答案
相关题目
2.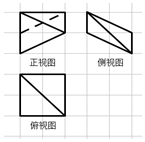 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
17.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}<1$”是“a>1”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | 设随机变量X~N(1,52),若P(X<0)=P(X>a-2),则实数a的值为2 |
1.2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
(${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
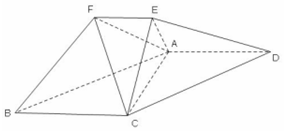 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,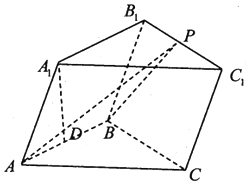 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.