题目内容
已知复数z=1+ai(a∈R)(i是虚数单位)在复平面上表示的点在第四象限,且|z|=
,则a=( )
| 5 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点:复数求模
专题:数系的扩充和复数
分析:由复数z=1+ai(a∈R)(i是虚数单位)在复平面上表示的点在第四象限得到a<0,再由|z|=
列式求得a的值.
| 5 |
解答:
解:∵复数z=1+ai(a∈R)(i是虚数单位)在复平面上表示的点在第四象限,
则a<0.
由|z|=
,得
=
,解得a=-2.
故选:B.
则a<0.
由|z|=
| 5 |
| 1+a2 |
| 5 |
故选:B.
点评:本题考查了复数的代数表示法及其集合意义,考查了复数模的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A,B,C三点不共线,空间内任一点O满足
=x
+y
+z
(x,y,z∈R),则“x+y+z=1”是“点P在由A,B,C所确定的平面内”的( )
| OP |
| OA |
| OB |
| OC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
等比数列{an}的首项a1=-1,前n项和为Sn若
=
,则公比q等于( )
| S 10 |
| S 5 |
| 31 |
| 32 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
用秦九韶算法求当x=1.032时多项式f(x)=3x2+2x+3的值时,需要m次乘法运算,n次加法运算,m,n分别为( )
| A、3,2 | B、4,3 |
| C、2,2 | D、2,3 |
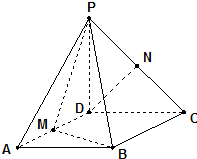 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.