题目内容
向平面区域Ω={(x,y)|0≤x≤π,-1≤y≤1}投掷一点P,则点P落入区域M={(x,y)|y>cosx,0≤x≤π}的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:作出对应的平面区域,求出对应的面积,利用几何槪型的概率公式计算即可得到结论.
解答:
解: 平面区域Ω={(x,y)|0≤x≤π,-1≤y≤1}对应的区域为矩形ABCD,面积S=2π,
平面区域Ω={(x,y)|0≤x≤π,-1≤y≤1}对应的区域为矩形ABCD,面积S=2π,
区域M={(x,y)|y>cosx,0≤x≤π}对应的区域为阴影部分,
则由余弦函数的对称性可知,阴影部分的面积S=
SABCD=π,
故点P落入区域M={(x,y)|y>cosx,0≤x≤π}的概率为
,
故选:B.
 平面区域Ω={(x,y)|0≤x≤π,-1≤y≤1}对应的区域为矩形ABCD,面积S=2π,
平面区域Ω={(x,y)|0≤x≤π,-1≤y≤1}对应的区域为矩形ABCD,面积S=2π,区域M={(x,y)|y>cosx,0≤x≤π}对应的区域为阴影部分,
则由余弦函数的对称性可知,阴影部分的面积S=
| 1 |
| 2 |
故点P落入区域M={(x,y)|y>cosx,0≤x≤π}的概率为
| 1 |
| 2 |
故选:B.
点评:本题主要考查几何槪型的概率计算,求出对应的面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
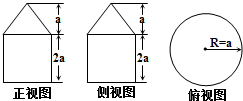 已知一个几何体的三视图如图所示,则此几何体的侧面积是( )
已知一个几何体的三视图如图所示,则此几何体的侧面积是( )| A、4πa2 | ||
| B、5πa2 | ||
C、(4+
| ||
D、(5+
|
执行如图所示的程序框图,输出的S值为-4时,则输入的S0的值为( )


| A、7 | B、8 | C、9 | D、10 |
(
)2014=( )
| 1+i |
| 1-i |
| A、i | B、-1 | C、1 | D、-i |
已知集合A={x|x2-x≤0},函数f(x)=2-x(x∈A)的值域为B,则(∁RA)∩B为( )
| A、(1,2] |
| B、[1,2] |
| C、[0,1] |
| D、(1,+∞) |
已知向量
=(sin(α+
),1),
=(1,cosα-
),若
⊥
,则sin(α+
)等于( )
| a |
| π |
| 6 |
| b |
| 3 |
| a |
| b |
| π |
| 3 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|