题目内容
18.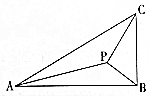 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
分析 由题意设∠PBA=α,在Rt△PBC中求出PB,在△PBA中,由∠APB=150°和内角和定理求出∠PAB,由正弦定理列出方程,由两角差的正弦函数化简后,由商的关系求出tan∠PBA的值.
解答  解:由题意知:
解:由题意知:
∠ABC=∠BPC=90°,AB=2$\sqrt{3}$,BC=2
设∠PBA=α,在Rt△PBC中,
PB=BCcos(90°-α)=2sinα,
在△PBA中,∠APB=150°,则∠PAB=30°-α,
由正弦定理得,$\frac{AB}{sin∠APB}=\frac{PB}{sin∠PAB}$,
则$\frac{2\sqrt{3}}{\frac{1}{2}}=\frac{2sinα}{sin(30°-α)}$,即$\frac{sinα}{sin(30°-α)}=2\sqrt{3}$,
sinα=2$\sqrt{3}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα),
化简得4sinα=$\sqrt{3}$cosα,则tanα=$\frac{\sqrt{3}}{4}$,
所以tan∠PBA=$\frac{\sqrt{3}}{4}$,
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题考查正弦定理,两角差的正弦函数,以及商的关系的应用,考查分析问题、解决问题的能力.

练习册系列答案
相关题目
10.已知全集U={1,2,3,4,5},集合A={4,5},则∁UA=( )
| A. | {5} | B. | {4,5} | C. | {1,2,3} | D. | {1,2,3,4,5} |
11.设a∈(0,5),且a≠1,则函数f(x)=loga(ax-1)在(2,+∞)上为单调函数的概率为( )
| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
13.已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=$\frac{1}{2}$f($\frac{1}{2}$),b=-2f(-2),c=ln$\frac{1}{2}$f(-ln 2),则下列关于a,b,c的大小关系正确的是( )
| A. | a>b>c | B. | a<c<b | C. | c>b>a | D. | b>a>c |
7.已知m、n、s、t∈R*,m+n=3,$\frac{m}{s}+\frac{n}{t}=1$其中m、n是常数且m<n,若s+t的最小值 是$3+2\sqrt{2}$,满足条件的点(m,n)是椭圆$\frac{x^2}{4}+\frac{y^2}{16}=1$一弦的中点,则此弦所在的直线方程为( )
| A. | x-2y+3=0 | B. | 4x-2y-3=0 | C. | x+y-3=0 | D. | 2x+y-4=0 |
8.为了得到函数y=sin(2x-$\frac{π}{3}$)的图象,只需把函数y=cos(2x-$\frac{4π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
 如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?
如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?