题目内容

8．已知x=0是函数f（x）=（x-2a）（x2+a2x+2a3）的极小值点，则实数a的取值范围是（-∞，0）∪（2，+∞）．

分析 求出函数的导数，问题转化为x＜0时，f′（x）=3x2+2（a2-2a）x＜0恒成立，得到关于a的不等式，解出即可．

解答 解：f（x）=（x-2a）（x2+a2x+2a3）=x3+（a2-2a）x2-4a4，
故f′（x）=3x2+2（a2-2a）x，
x=0是函数f（x）的极小值点，
则x＜0时，f′（x）=3x2+2（a2-2a）x＜0恒成立，
即2（a2-2a）＞0，解得：a＞2或a＜0，
故答案为：（-∞，0）∪（2，+∞）．

点评 本题考查了函数的单调性、极值问题，考查导数的应用，是一道中档题．

练习册系列答案
相关题目
20．如图，一个正六角星薄片（其对称轴与水面垂直）匀速地升出水面，直到全部露出水面为止，记时刻t薄片露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S'（t）的图象大致为（　　）
A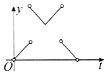．B．C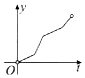．D．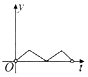
1．曲线y=x3+2x+1在点P（1，4）处的切线与y轴交点的纵坐标是（　　）
A．-9B．-3C．-1D．3
18．在△ABC中，角A，B，C所对的边长分别为a，b，c，且满足csinB=$\sqrt{3}$bcosC，a2-c2=2b2
（Ⅰ）求C的大小；
（Ⅱ）若△ABC的面积为21$\sqrt{3}$，求b的值．
3．已知函数f（x）=x-alnx，g（x）=-$\frac{1+a}{x}$，其中a∈R
（1）设函数h（x）=f（x）-g（x），求函数h（x）的单调区间；
（2）若存在x0∈[1，e]，使得f（x0）＜g（x0）成立，求a的取值范围．
13．已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+$\frac{f（x）}{x}$＞0，若a=$\frac{1}{2}$f（$\frac{1}{2}$），b=-2f（-2），c=ln$\frac{1}{2}$f（-ln 2），则下列关于a，b，c的大小关系正确的是（　　）
A．a＞b＞cB．a＜c＜bC．c＞b＞aD．b＞a＞c
20．已知x=$\frac{π}{12}$是函数f（x）=$\sqrt{3}$sin（2x+φ）+cos（2x+φ）（0＜φ＜π）图象的一条对称轴，将函数f（x）的图象向右平移$\frac{3π}{4}$个单位后得到函数g（x）的图象，则函数g（x）在[-$\frac{π}{4}$，$\frac{π}{6}$]上的最小值为（　　）
A．-2B．-1C．-$\sqrt{2}$D．-$\sqrt{3}$
17．一次测试中，为了了解学生的学习情况，从中抽取了n个学生的成绩进行统计．按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在的数据）．

（1）求样本容量n和频率分布直方图中x，y的值；
（2）求这n名同学成绩的平均数、中位数及众数；
（3）在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取3名参加志愿者活动，所抽取的3名同学中至少有一名成绩在[90，100]内的概率．
18．设函数$f（x）=ln（{x+1}）+\frac{1}{2}a{x^2}-x$，其中a∈R．
（Ⅰ）当a=2时，讨论函数f（x）的单调性，并说明理由；
（Ⅱ）若?x＞0，f（x）≥ax-x成立，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网