题目内容
8.已知菱形ABCD,若|$\overrightarrow{AB}$|=1,A=$\frac{π}{3}$,则向量$\overrightarrow{AC}$在$\overrightarrow{AB}$上的投影为$\frac{3}{2}$.分析 由题意作图辅助,解菱形,从而求得向量$\overrightarrow{AC}$在$\overrightarrow{AB}$上的投影.
解答 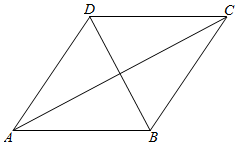 解:∵在菱形ABCD中,A=$\frac{π}{3}$,
解:∵在菱形ABCD中,A=$\frac{π}{3}$,
∴∠CAB=$\frac{π}{6}$,
又∵|$\overrightarrow{AB}$|=1,
∴|$\overrightarrow{AC}$|=2|$\overrightarrow{AB}$|cos$\frac{π}{6}$=$\sqrt{3}$,
∴向量$\overrightarrow{AC}$在$\overrightarrow{AB}$上的投影为|$\overrightarrow{AC}$|cos$\frac{π}{6}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了数形结合的思想方法应用及平面向量的应用,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{\frac{x}{2}}-1,0<x≤4}\\{|x-7|,x>4}\end{array}\right.$,若方程f(x)=kx+1有三个不同的实数根,则实数k的取值范围是( )
| A. | (-$\frac{1}{7}$,$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{7}$)∪($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{7}$,$\frac{1}{2}$) | D. | (-$\frac{1}{7}$,$\frac{1}{2}$] |
16.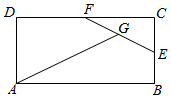 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
则$\overrightarrow{AG}$=( )
 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |
17.已知集合A={x|x2+2x-3≥0},B={x|-2≤x<2},则A∩B=( )
| A. | [-2,-1] | B. | [-1,2) | C. | [-2,1] | D. | [1,2) |