题目内容
16.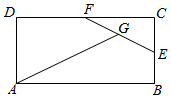 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |
分析 建立平面直角坐标系,利用平面向量的坐标表示,列出方程组,即可求出$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$中的x与y的值.
解答 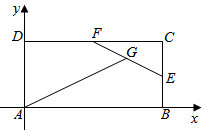 解:建立平面直角坐标系,如图所示;
解:建立平面直角坐标系,如图所示;
矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
设B(2,0),则D(0,1),E(2,$\frac{1}{2}$),F(1,1),
∴G($\frac{3}{2}$,$\frac{3}{4}$);
∴$\overrightarrow{AG}$=($\frac{3}{2}$,$\frac{3}{4}$),$\overrightarrow{AB}$=(2,0),$\overrightarrow{AD}$=(0,1),
设$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,
则($\frac{3}{2}$,$\frac{3}{4}$)=(2x,y),
即$\left\{\begin{array}{l}{2x=\frac{3}{2}}\\{y=\frac{3}{4}}\end{array}\right.$,
解得x=$\frac{3}{4}$,y=$\frac{3}{4}$;
∴$\overrightarrow{AG}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$.
故选:C.
点评 本题考查了平面向量的线性表示与运算问题,也考查了数形结合的解题思想,是基础题目.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
6.已知f(x)=m•2x+x2+nx,若{x|f(x)=0}={x|f(f(x))=0}≠∅,则m+n的取值范围为( )
| A. | (0,4) | B. | [0,4) | C. | (0,5] | D. | [0,5] |
1.在△ABC中,a,b,c分别是内角A,B,C的对边,若bsinA=3csinB,a=3,$cosB=\frac{2}{3}$,则b=( )
| A. | 14 | B. | 6 | C. | $\sqrt{14}$ | D. | $\sqrt{6}$ |