题目内容
2.某几何体的三视图如图所示,则该几何体的表面积为( )
| A. | 12+4$\sqrt{3}$ | B. | 12 | C. | $8+2\sqrt{3}$ | D. | 8 |
分析 由三视图还原原图形如图,然后利用三角形面积公式求解.
解答 解:由三视图可得原几何体如图,
AB=BC=BE=DF=2,
则△AEC与△AFC边AC上的高为$\sqrt{{2}^{2}+(\sqrt{2})^{2}}=\sqrt{6}$,
∴该几何体的表面积为S=$2×2+4×\frac{1}{2}×2×2+2×\frac{1}{2}×2\sqrt{2}×\sqrt{6}$=$12+4\sqrt{3}$.
故选:A.
点评 本题考查空间几何体的三视图,由三视图还原原图形是关键,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.某程序框图如图所示,若运行该程序后输出的值是$\frac{9}{19}$,则整数t的值是( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
14.已知命题$p:?x∈R,{({\frac{1}{10}})^x}≤0$,若(¬p)∧q是假命题,则命题q可以是( )
| A. | 函数y=-2x2+x在[1,3)上单调递减 | B. | ln3>1 | ||
| C. | 若A∩B=A,则B⊆A | D. | lg2+lg3=lg5 |
11.一个几何体的三视图如图所示,则此几何体的体积为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
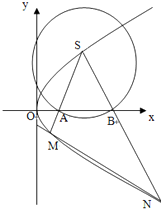 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.