题目内容

10．已知函数f（x）=x2+3，则f（x）在（2，f（2））处的切线方程为4x-y-1=0．

分析 求出函数f（x）的导函数，得到f′（2），再求出f（2），代入直线方程的点斜式得答案．

解答 解：由f（x）=x2+3，得f′（x）=2x，
∴f′（2）=4，
又f（2）=7，
∴f（x）在（2，f（2））处的切线方程为y-7=4（x-2），
即4x-y-1=0．
故答案为：4x-y-1=0．

点评 本题考查利用导数研究过曲线上某点处的切线方程，过曲线上某点处的切线的斜率，就是函数在该点处的导数值，是基础题．

练习册系列答案
相关题目
20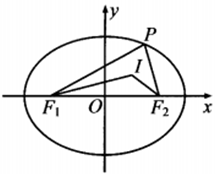．设P为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的动点，F1、F2为椭圆C的焦点，I为△PF1F2的内心，则直线IF1和直线IF2的斜率之积（　　）
A．是定值B．非定值，但存在最大值
C．非定值，但存在最小值D．非定值，且不存在最值
1．在△ABC中，内角A，B，C的对边分别为a，b，c，且$\frac{b}{a}$=$\frac{\sqrt{3}cosB}{sinA}$．
（Ⅰ）求角B的大小；
（Ⅱ）若b=2$\sqrt{3}$，△ABC的面积为2$\sqrt{3}$，求△ABC的周长．
18．用反证法证明命题“三角形的内角中至少有一个不大于60°”时，假设命题的结论不成立的正确叙述是②（填序号）．
①假设三个角都不大于60°；         ②假设三个角都大于60°；
③假设三个角至多有一个大于60°；    ④假设三个角至多有两个大于60°．
5．在平面直角坐标系xOy中，抛物线y2=4x的焦点为F，准线交x轴于点H，过H作直线l交抛物线于A，B两点，且|BF|=2|AF|，则△ABF的面积为$\sqrt{2}$．
15．已知定义域为R的奇函数y=f（x）的导函数为y=f'（x），当x≠0时，$f'（x）+\frac{f（x）}{x}＞0$，若$a=\frac{1}{2}f（{\frac{1}{2}}）$，b=-2f（-2），$c=（{ln\frac{1}{2}}）f（{ln\frac{1}{2}}）$，则a，b，c的大小关系正确的是a＜c＜b．
2．化简$2\sqrt{1-sin10}+\sqrt{2+2cos10}$的结果是（　　）
A．4cos5-2sin5B．-2sin5-4cos5C．2sin5-4cos5D．-2sin5
5．已知f（x）=ln（$\frac{1+x}{1-x}$），若∨x∈[0，1），f（x）≥ax恒成立，求实数a的取值范围．
6．已知数列{an}的首项a1=3，an+1=2an+1（n∈N*）．
（Ⅰ）写出数列{an}的前5项，并归纳猜想{an}的通项公式；
（Ⅱ）用数学归纳法证明（Ⅰ）中所猜想的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网