题目内容
20.设$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$是任意的非零向量,且相互不平行,则下面四个命题:①$(\overrightarrow a•\overrightarrow b)\overrightarrow c-(\overrightarrow c•\overrightarrow a)\overrightarrow b=\overrightarrow 0$;
②$|{\overrightarrow a}|-|{\overrightarrow b}|<|{\overrightarrow a-\overrightarrow b}|$;
③$(\overrightarrow b•\overrightarrow c)\overrightarrow a-(\overrightarrow c•\overrightarrow a)\overrightarrow b$不与$\overrightarrow c$垂直;
④$(3\overrightarrow a+2\overrightarrow b)•(3\overrightarrow a-2\overrightarrow b)=9{|{\overrightarrow a}|^2}-4{|{\overrightarrow b}|^2}$.
其中是真命题的为( )
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ②④ |
分析 ①,$(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{c}$是与$\overrightarrow{c}$共线的向量,$(\overrightarrow{c}•\overrightarrow{a})\overrightarrow{b}$是与$\overrightarrow{b}$共线的向量;
②,由向量减法的三角形法则,及三角形的两边之差小于第三边可知;
③,[$(\overrightarrow b•\overrightarrow c)\overrightarrow a-(\overrightarrow c•\overrightarrow a)\overrightarrow b$]•$\overrightarrow c$=0,;
④,$(3\overrightarrow a+2\overrightarrow b)•(3\overrightarrow a-2\overrightarrow b)=9{|{\overrightarrow a}|^2}-4{|{\overrightarrow b}|^2}$成立;
解答 解:设$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$是任意的非零向量,且相互不平行:
对于①,$(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{c}$是与$\overrightarrow{c}$共线的向量,$(\overrightarrow{c}•\overrightarrow{a})\overrightarrow{b}$是与$\overrightarrow{b}$共线的向量故$(\overrightarrow a•\overrightarrow b)\overrightarrow c-(\overrightarrow c•\overrightarrow a)\overrightarrow b=\overrightarrow 0$错;
对于②,由向量减法的三角形法则,及三角形的两边之差小于第三边知$|{\overrightarrow a}|-|{\overrightarrow b}|<|{\overrightarrow a-\overrightarrow b}|$,正确;
对于③,∵[$(\overrightarrow b•\overrightarrow c)\overrightarrow a-(\overrightarrow c•\overrightarrow a)\overrightarrow b$]•$\overrightarrow c$=0,故错;
对于④,$(3\overrightarrow a+2\overrightarrow b)•(3\overrightarrow a-2\overrightarrow b)=9{|{\overrightarrow a}|^2}-4{|{\overrightarrow b}|^2}$,正确;
故选:D.
点评 本题考查了命题真假的判定,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | 如果平面α⊥平面β,任取直线m?α,那么必有m⊥β | |
| B. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| C. | 如果直线m∥平面α,直线n∥平面α,那么m∥n | |
| D. | 如果平面α外的一条直线m垂直于平面α内的两条相交直线,那么m⊥α |
| A. | -$\frac{1}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
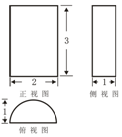
| A. | 4π | B. | 5π+6 | C. | 3π+6 | D. | 4π+6 |
 如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.
如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD. 已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).
已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).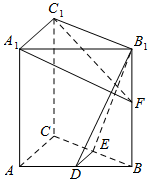 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证: