题目内容
15. 已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).
已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).(1)当以{$\overrightarrow{AB}$,$\overrightarrow{AD}$}为基底时,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,
用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$;
用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AE}$=$\frac{3}{4}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$;
(2)设点MN分别为边DC,BC中点.
①当以{$\overrightarrow{AB}$,$\overrightarrow{AD}$}为基底时,设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,
用$\overrightarrow{c}$,$\overrightarrow{d}$表示$\overrightarrow{AN}$,则$\overrightarrow{AN}$=$\overrightarrow{c}$+$\frac{1}{2}\overrightarrow{d}$.
②当以{$\overrightarrow{AM}$,$\overrightarrow{AN}$}为基底时,设$\overrightarrow{AM}$=$\overrightarrow{m}$,$\overrightarrow{AN}$=$\overrightarrow{n}$,用$\overrightarrow{m}$,$\overrightarrow{n}$表示:
$\overrightarrow{AB}$=$\frac{4}{3}\overrightarrow{n}-\frac{2}{3}\overrightarrow{m}$,$\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{n}+\frac{2}{3}\overrightarrow{m}$,$\overline{OE}$=$\frac{1}{2}\overrightarrow{n}+\frac{1}{2}\overrightarrow{m}$.
分析 利用向量的三角形法则、平行四边形法则逐一求解.
解答 解:(1)$\overrightarrow{OD}$=$\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{AD}-\overrightarrow{AB})=\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$;$\overrightarrow{AE}=\frac{1}{2}(\overrightarrow{AO}+\overrightarrow{AB})$,$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})$,∴$\overrightarrow{AE}=\frac{3}{4}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$;
(2)①依题意$\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{c}+\frac{1}{2}\overrightarrow{d}$;
②$2\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{AC}=2\overrightarrow{AD}+\overrightarrow{AB}$,$2\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}+2\overrightarrow{AB}$;
⇒$\overrightarrow{AB}=\frac{4}{3}\overrightarrow{AN}-\frac{2}{3}\overrightarrow{AM}=\frac{4}{3}\overrightarrow{n}-\frac{2}{3}\overrightarrow{m}$,$\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AM}-\frac{2}{3}\overrightarrow{AN}=\frac{4}{3}\overrightarrow{m}-\frac{2}{3}\overrightarrow{n}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=\frac{2}{3}\overrightarrow{m}+\frac{2}{3}\overrightarrow{n}$;
$\overrightarrow{OE}=\frac{1}{4}\overrightarrow{DB}=\frac{1}{4}(\overrightarrow{AB}-\overrightarrow{AD})=\frac{1}{2}\overrightarrow{n}-\frac{1}{2}\overrightarrow{m}$.
点评 本题考查了向量的线性运算,熟练运用三角形法则是解题关键,属于基础题.

| A. | [1,+∞) | B. | (1,+∞) | C. | $[\frac{1}{2e-1},+∞)$ | D. | $(\frac{1}{2e-1},+∞)$ |
| A. | $({0,4-2\sqrt{2}})$ | B. | $({4-2\sqrt{2},2})$ | C. | $({4-2\sqrt{2},\frac{4}{3}}]$ | D. | $({\frac{4}{3},2}]$ |
| A. | y=sin|x| | B. | y=sin2x | C. | y=-sinx | D. | y=sinx+1 |

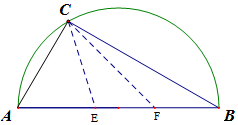 如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.