题目内容
12．已知二阶矩阵M有特征值λ=8及对应的一个特征向量$\overrightarrow{e_1}=[\begin{array}{l}1\\ 1\end{array}]$，并且矩阵M将点（-1，3）变换为（0，8）．求矩阵M．分析 设出矩阵，利用特征向量的定义，即二阶变换矩阵的概念，建立方程组，即可得到结论．
解答 解：设$M=[{\begin{array}{l}a&b\\ c&d\end{array}}]$，由$[{\begin{array}{l}a&b\\ c&d\end{array}}][{\begin{array}{l}1\\ 1\end{array}}]=8[{\begin{array}{l}1\\ 1\end{array}}]$及$[{\begin{array}{l}a&b\\ c&d\end{array}}][{\begin{array}{l}{-1}\\ 3\end{array}}]=[{\begin{array}{l}0\\ 8\end{array}}]$，…（5分）
得$\left\{\begin{array}{l}a+b=8\\ c+d=8\\-a+3b=0\\-c+3d=8\end{array}\right.$，解得$\left\{\begin{array}{l}a=6\\ b=2\\ c=4\\ d=4\end{array}\right.$，∴$M=[{\begin{array}{l}6&2\\ 4&4\end{array}}]$…（10分）
点评 本题考查特征值，考查二阶变换矩阵，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
2．设函数f（x）=x2+bx+c（b，c∈R），若对任意x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，则b的取值范围是（ ）
| A． | [0，2] | B． | （0，2] | C． | （-2，2） | D． | [-2，2] |
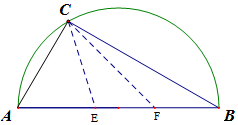如图，有一直径为8米的半圆形空地，现计划种植果树，但需要有辅助光照．半圆周上的C处恰有一可旋转光源满足果树生长的需要，该光源照射范围是$∠ECF=\frac{π}{6}$，点E，F在直径AB上，且$∠ABC=\frac{π}{6}$．
17．函数y=e|-lnx|-|x-1|的图象大致是（ ）
| A． |  | B． |  | C． |  | D． |  |