题目内容
18.若k∈R,则“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
分析 方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆?$\left\{\begin{array}{l}{k-1>0}\\{k+1>0}\\{k-1≠k+1}\end{array}\right.$,解得k,即可判断出结论.
解答 解:方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆?$\left\{\begin{array}{l}{k-1>0}\\{k+1>0}\\{k-1≠k+1}\end{array}\right.$,解得k>1.
∴“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的充要条件.
故选:C.
点评 本题考查了椭圆的标准方程及其性质、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.已知实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$且ax-y+1-a=0,则实数a的取值范围是( )
| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
6.若平面α,β,γ中,α⊥β,则“γ⊥β”是“α∥γ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知抛物线C:y2=8x,直线l:y=$\frac{{\sqrt{3}}}{3}$(x-2),直线l交C于A,B两点,则|AB|等于( )
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
8.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=1,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
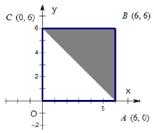 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).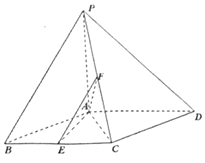 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.