题目内容
3.已知抛物线C:y2=8x,直线l:y=$\frac{{\sqrt{3}}}{3}$(x-2),直线l交C于A,B两点,则|AB|等于( )| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
分析 把直线y=$\frac{{\sqrt{3}}}{3}$(x-2),代入抛物线y2=8x,再利用弦长公式求解.
解答 解:把直线y=$\frac{{\sqrt{3}}}{3}$(x-2),代入抛物线y2=8x,
得$\frac{1}{3}$(x-2)2=8x,
整理,得x2-28x+4=0,
设A(x1,y1),B(x2,y2),
x1+x2=28,x1x2=4,
∴|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=32.
故选:C.
点评 本题考查直线与抛物线相交弦弦长的求法,是基础题,解题时发注意弦长公式的灵活运用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
13.在等比数列{an}中,已知a3=6,a3+a5+a7=78,则a5=( )
| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
18.若k∈R,则“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
15.在等差数列{an}中,若a3+a11=6,则其前13项的和S13的值是( )
| A. | 32 | B. | 39 | C. | 46 | D. | 78 |
12.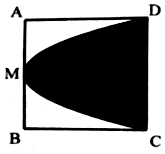 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |