题目内容
9.已知实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$且ax-y+1-a=0,则实数a的取值范围是( )| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
分析 画出约束条件的可行域,化简目标函数,推出a的表达式,利用不等式的几何意义,求解范围即可.
解答  解:实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$的可行域如图:可知x≤-1,
解:实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$的可行域如图:可知x≤-1,
由ax-y+1-a=0,可得:a=$\frac{y-1}{x-1}$,它的几何意义是可行域内的点与D(1,1)连线的斜率,由图形可知连线的斜率的最大值为KBD=$\frac{0-1}{-1-1}$=$\frac{1}{2}$.最小值大于与直线x+y=0平行时的斜率.
可得a∈(-1,$\frac{1}{2}$].
故选:C.
点评 本题考查线性规划的应用,化简目标函数判断目标函数的几何意义是解题的关键.

练习册系列答案
相关题目
19.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,如图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面叙述不正确的是( )
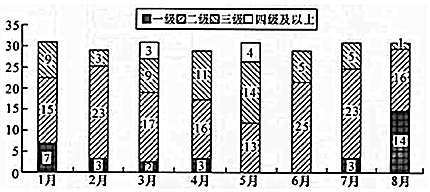

| A. | 1月至8月空气合格天数超过20天的月份有5个 | |
| B. | 第二季度与第一季度相比,空气达标天数的比重下降了 | |
| C. | 8月是空气质量最好的一个月 | |
| D. | 6月份的空气质量最差 |
20.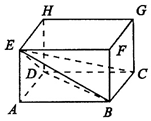 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
4.已知集合A={1,2,3},B={x∈Z|(x+2)(x-3)<0},则A∪B( )
| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
18.若k∈R,则“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |