题目内容
10.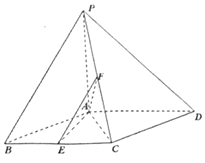 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.(Ⅰ)证明:AE⊥PD;
(Ⅱ)设AB=1,PD与平面ABCD所成的角为$\frac{π}{4}$,求二面角E-AF-C的正弦值.
分析 (Ⅰ)推导出AE⊥BC,AE⊥AD,PA⊥AE,从而AE⊥平面PAD,由此能证明AE⊥PD.
(Ⅱ)由AE,AD,AP,两两垂直,以A为坐标原点,建立空间直角坐标系,二面角E-AF-C的正弦值.
解答 证明:(Ⅰ)由四边形ABCD为菱形,∠ABC=60°,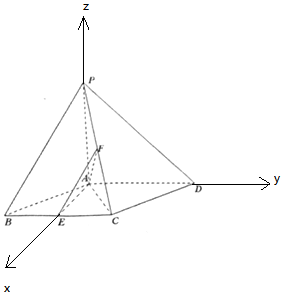
可得△ABC为正三角形.
∵E为BC的中点,∴AE⊥BC.
又BC∥AD,因此AE⊥AD.
∵PA⊥平面ABCD,∴PA⊥AE
而PA∩AD=A,∴AE⊥平面PAD,又PD?平面PAD
∴AE⊥PD.
解:(Ⅱ)由PA⊥平面ABCD,PD,
则在面ABCD射影为AD,
即∠PDA是PD与平面ABCD所成的角,
∴∠PDA=45°,AP=AD=1
由(Ⅰ)知AE,AD,AP,两两垂直,以A为坐标原点,
建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,
∴$A(0,0,0),E(\frac{{\sqrt{3}}}{2},0,0),P(0,0,1),C(\frac{{\sqrt{3}}}{2},\frac{1}{2},0),F(\frac{{\sqrt{3}}}{4},\frac{1}{4},\frac{1}{2})$,
$B(\frac{{\sqrt{3}}}{2},-\frac{1}{2},0)D(0,1,0)$,
∴$\overrightarrow{AE}=(\frac{{\sqrt{3}}}{2},0,0),\overrightarrow{AF}=(\frac{{\sqrt{3}}}{4},\frac{1}{4},\frac{1}{2})$.
设平面AEF的一法向量为$\overrightarrow n=({x_1},{y_1},{z_1})$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AE}=0\\ \overrightarrow n•\overrightarrow{AF}=0\end{array}\right.$,$\left\{\begin{array}{l}\frac{{\sqrt{3}}}{2}{x_1}=0\\ \frac{{\sqrt{3}}}{4}{x_1}+\frac{1}{4}{y_1}+\frac{1}{2}{z_1}=0.\end{array}\right.$
令z1=1,则$\overrightarrow n=(0,-2,1)$,
而ABCD是棱形,∴AC⊥BD,又BD⊥PA.PA∩AC=A,
∴BD⊥平面AFC.
$\overrightarrow{BD}=(-\frac{{\sqrt{3}}}{2},\frac{3}{2,}0)$为平面AFC的一个法向量.
∴$cos<\overrightarrow n,\overrightarrow{BD}>=\frac{{\overrightarrow n•\overrightarrow{BD}}}{{|\overrightarrow{n|}•|\overrightarrow{BD}|}}=\frac{-3}{{\sqrt{5}×\sqrt{3}}}=\frac{{\sqrt{15}}}{5}$,
∵$sin<\overrightarrow n,\overrightarrow{BD}>$=$\sqrt{1-(\frac{\sqrt{15}}{5})^{2}}$=$\frac{\sqrt{10}}{5}$,
∴二面角E-AF-C的正弦值为$\frac{{\sqrt{10}}}{5}$.
点评 本题考查线线垂直的证明,考查二面角的正弦值的求法,是中档题,注意向量法的合理运用.

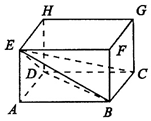 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
| A. | $\frac{3}{2}$ | B. | 0 | C. | 2 | D. | $-\frac{3}{2}$ |
| A. | 32 | B. | 39 | C. | 46 | D. | 78 |
| 不喜欢戏剧 | 喜欢戏剧 | |
| 男性青年观众 | 40 | 10 |
| 女性青年观众 | 40 | 60 |