题目内容
8.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=1,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 根据平面向量的数量积运算公式,代入计算即可求出$\overrightarrow{a}$、$\overrightarrow{b}$的夹角.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,
且($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=1,
∴${\overrightarrow{a}}^{2}$-$\overrightarrow{b}$•$\overrightarrow{a}$=1,
∴22-3×2×cos<$\overrightarrow{b}$,$\overrightarrow{a}$>=1,
解得cos<$\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{1}{2}$,
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故选:C.
点评 本题考查了平面向量的数量积与夹角公式的计算问题,是基础题.

练习册系列答案
相关题目
18.若k∈R,则“k>1”是方程“$\frac{x^2}{k-1}+\frac{y^2}{k+1}=1$”表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
16.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(c,0),过点F且垂直于x轴的直线在第一象限内与双曲线及双曲线的渐近线的交点依次为A、B,若2$\overrightarrow{OA}$=$\overrightarrow{OB}$+$\overrightarrow{OF}$,则该双曲线的离心率的值为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
20.下表是关于青年观众的性别与是否喜欢戏剧的调查数据,人数如表所示:
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调研,若在“不喜欢戏剧的男性青年观众”的人中抽取了8人,则n的值为30.
| 不喜欢戏剧 | 喜欢戏剧 | |
| 男性青年观众 | 40 | 10 |
| 女性青年观众 | 40 | 60 |
17.已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的直径,△ABC是边长为4的等边三角形,三棱椎P-ABC的体积为$\frac{16}{3}$,则该三棱锥的外接球的表面积为( )
| A. | $\frac{16π}{3}$ | B. | $\frac{40π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{80π}{3}$ |
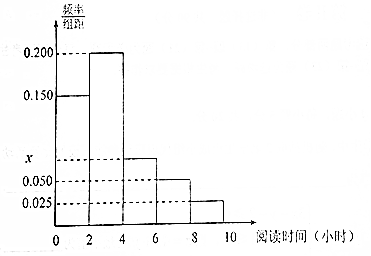 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图: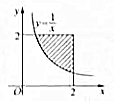 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.