题目内容
3.在△ABC中,O为其内部一点,且满足$\overrightarrow{OA}+\overrightarrow{OC}+3\overrightarrow{OB}=\vec 0$,则△AOB和△AOC的面积比是( )| A. | 3:4 | B. | 3:2 | C. | 1:1 | D. | 1:3 |
分析 设M为AC的中点,则由向量加法的平行四边形法则可得$\overrightarrow{OA}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$,结合题意可得2$\overrightarrow{OM}$=-3$\overrightarrow{OM}$,由数乘向量的性质可得B,O,M三点共线,且2OM=3BO;进而可得$\frac{{S}_{△AOC}}{{S}_{△ABC}}$=$\frac{OM}{BM}$=$\frac{3}{5}$,而又由S△AOB+S△BOC=$\frac{2}{5}$S△ABC,分析可得S△AOB=$\frac{1}{5}$S△ABC,结合题意计算可得△AOB和△AOC的面积比,即可得答案.
解答 解:根据题意, 如图:在△ABC中,M为AC的中点,
如图:在△ABC中,M为AC的中点,
则$\overrightarrow{OA}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$,
又由$\overrightarrow{OA}+\overrightarrow{OC}+3\overrightarrow{OB}=\vec 0$,则有2$\overrightarrow{OM}$=-3$\overrightarrow{OB}$,
从而可得B,O,M三点共线,且2OM=3BO;
由2OM=3BO可得,$\frac{{S}_{△AOC}}{{S}_{△ABC}}$=$\frac{OM}{BM}$=$\frac{3}{5}$,
S△AOB+S△BOC=$\frac{2}{5}$S△ABC,
又由S△AOB=S△BOC,则S△AOB=$\frac{1}{5}$S△ABC,
则$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=$\frac{1}{3}$;
故选:D.
点评 本题考查向量的加法运算及其几何意义,向量的共线与点共线的相互转化,解题的关键是要发现由2OM=3BO.

| A. | (-1,+∞) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,1) |
| A. | 0.48 | B. | 0.6 | C. | 0.75 | D. | 0.8 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
| A. | $\frac{4π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{32π}{3}$ |
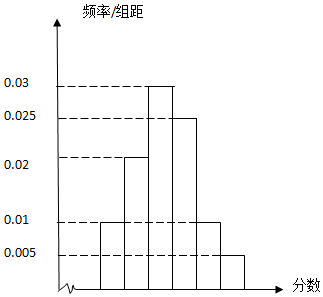 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示(I)用每组区间的中点值代表该组的数据,估算这批考生的平均成绩;
(II)现从及格的学生中,用分层抽样的方法抽取了70名学生(其中女生有34名),已知成绩“优异”(超过90分)的女生有1名,能否有95%的把握认为数学成绩优异与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | $0<a<\frac{1}{2}$ | B. | $\frac{1}{3}<a<\frac{1}{2}$ | C. | $0<a<\frac{1}{3}$ | D. | a>1或$0<a<\frac{1}{3}$ |