题目内容
11.2016年鞍山地区空气质量的记录表明,一天的空气质量为优良的概率为0.8,连续两天为优良的概率为0.6,若今天的空气质量为优良,则明天空气质量为优良的概率是( )| A. | 0.48 | B. | 0.6 | C. | 0.75 | D. | 0.8 |
分析 设随后一天的空气质量为优良的概率是p,利用相互独立事件概率乘法公式能求出结果.
解答 解:∵一天的空气质量为优良的概率为0.8,连续两天为优良的概率为0.6,
设随后一天空气质量为优良的概率为p,
若今天的空气质量为优良,则明天空气质量为优良,则有0.8p=0.6,
∴p=$\frac{0.6}{0.8}$=$\frac{3}{4}$=0.75,
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.函数y=kx+2与函数$y=\frac{1}{|x|}$的图象至少有两个公共点,关于k不等式(k-2)a-k>0有解,则实数a的取值范围是( )
| A. | $-1<a<\frac{1}{3}$ | B. | $a<\frac{1}{3}$ | C. | a<-1 | D. | a≥1 |
6.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得$\overrightarrow{OM}•\overrightarrow{OA}=\overrightarrow{OF}•\overrightarrow{OA}$,且$\overrightarrow{OM}+\overrightarrow{OF}=t\overrightarrow{OA}({t∈R})$,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
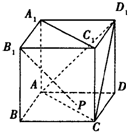 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在四边形ABCD内及其边界上运动,且点P到点B1的距离为$\sqrt{2}$.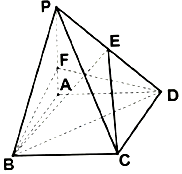 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2. 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法: