题目内容
13.已知函数$f(x)=\left\{\begin{array}{l}{a^x},\;0<x≤1\;\\{log_a}x\;,x>1\end{array}\right.$(a>0且a≠1),若f(3a2)>f(1-2a),则a的取值范围是( )| A. | $0<a<\frac{1}{2}$ | B. | $\frac{1}{3}<a<\frac{1}{2}$ | C. | $0<a<\frac{1}{3}$ | D. | a>1或$0<a<\frac{1}{3}$ |
分析 由题意,a>0且1-2a>0,得0<a<$\frac{1}{2}$,函数f(x)单调递减,利用f(3a2)>f(1-2a),3a2<1-2a,即可求出a的取值范围.
解答 解:由题意,a>0且1-2a>0,∴0<a<$\frac{1}{2}$,函数f(x)单调递减,
∵f(3a2)>f(1-2a),
∴3a2<1-2a,∴∴-1<a<$\frac{1}{3}$,
∴0<a<$\frac{1}{3}$,
故选C.
点评 本题考查a的取值范围,考查函数的单调性,考查学生解不等式的能力,正确转化是关键.

练习册系列答案
相关题目
3.在△ABC中,O为其内部一点,且满足$\overrightarrow{OA}+\overrightarrow{OC}+3\overrightarrow{OB}=\vec 0$,则△AOB和△AOC的面积比是( )
| A. | 3:4 | B. | 3:2 | C. | 1:1 | D. | 1:3 |
4.如图所示,在△ABC中,D为BC的中点,BP丄DA,垂足为P,且BP=2,则$\overrightarrow{BC}$•$\overrightarrow{BP}$=( )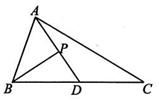

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
8.若i为虚数单位,则复数$\frac{1+i}{3-i}$等于( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{4}+\frac{1}{2}i$ | C. | $\frac{2}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
2.设圆:x2+y2+2y-3=0与y轴交于A(0,y1),B(0,y2)两点,则y1y2 的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |