题目内容
若f（x）=ax2+bx+c，不等式f（x）＞0的解集是{x|x1＜x＜x2}，f（0）＞0，则（ ）
| A、f（x1+x2）＞0 |
| B、f（x1+x2）＜0 |
| C、f（x1+x2）=0 |
| D、不能确定f（x1+x2）的符号 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：根据已知条件得到c＞0，a＜0，且x1，x2是ax2+bx+c=0的两个根，由韦达定理得到x1+x2=-
，再根据
f（x1+x2）=c，可得结论．
| b |
| a |
f（x1+x2）=c，可得结论．
解答：
解：由于f（0）=c＞0，ax2+bx+c＞0的解集是{x|x1＜x＜x2}，
∴a＜0，且 x1，x2是ax2+bx+c=0的两个根，由韦达定理得到x1+x2=-
，
由f（x1+x2）=a•(-
)2+b•（-
）+c-
=c＞0，
故选：A．
∴a＜0，且 x1，x2是ax2+bx+c=0的两个根，由韦达定理得到x1+x2=-
| b |
| a |
由f（x1+x2）=a•(-
| b |
| a |
| b |
| a |
| b2 |
| a |
故选：A．
点评：本题主要考查一元二次不等式的解法，韦达定理的应用，属于基础题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
常数列c，c，c，…，c，…（ ）
| A、一定是等差数列但不一定是等比数列 |
| B、一定是等比数列，但不一定是等差数列 |
| C、既一定是等差数列又一定是等比数列 |
| D、既不一定是等差数列，又不一定是等比数列 |
在直角坐标系中，已知点A（0，1）和点B（-3，4），若点P在∠AOB的平分线上且|
|=2，则点P的坐标为（ ）
| OP |
A、（-
| ||||||||
B、（-
| ||||||||
C、（-
| ||||||||
D、（-
|
定义运算a*b=
，例如1*2=1，则2*a的取值范围是（ ）
|
| A、（0，2） |
| B、（-∞，2] |
| C、[0，2] |
| D、[2，+∞） |
已知函数f（x）=|
-1|，若存在正实数a，b（a＜b），使得集合{y|y=f（x），a≤x≤b}=[ma，mb]，则m的取值范围为（ ）
| 1 |
| x |
A、（0，
| ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
已知集合A={x|x2-
x+1=0}，若A∩R=∅，则实数m的取值范围为（ ）
| m |
| A、m＜4 | B、m＞4 |
| C、0＜m＜4 | D、0≤m＜4 |
若函数f（x）在给定区间M上存在正数t，使得对于任意的x∈M，有x+t∈M，且f（x+t）≥f（x），则称f（x）为M上t级类增函数，则下列命题中正确的是（ ）
A、函数f（x）=
| ||||||
| B、函数f（x）=|log2（x-1）|是（1，+∞）上的1级类增函数 | ||||||
C、若函数f（x）=sinx+ax为[
| ||||||
| D、若函数f（x）=x2-3x为[1，+∞）上的t级类增函数，则实数t的取值范围为[2，+∞） |
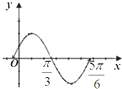
已知函数y=2sin（ωx+φ）（ω＞0，|φ|＜
）的图象的一部分如图所示，则（ ）
| π |
| 2 |
A、ω=2，φ=
| ||
B、ω=2，φ=-
| ||
C、ω=2，φ=
| ||
D、ω=2，φ=-
|