题目内容
1.空间四边形ABCD的各棱长和对角线均为a,E,F分别是BC,AD的中点,则异面直线AE,CF所成角的余弦值为$\frac{2}{3}$.分析 可考虑用空间向量求异面直线AE与CF所成角的余弦值,可设正四面体的棱长为1,cos<$\overrightarrow{AE}$,$\overrightarrow{CF}$>=$\frac{-\frac{1}{2}}{\frac{3}{4}}$=-$\frac{2}{3}$,这样便可得到异面直线AE与CF所成角的余弦值.
解答 解:$\overrightarrow{CF}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CD}$),$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{CB}$-$\overrightarrow{CA}$.
设正四面体的棱长为1,则|$\overrightarrow{AE}$|=|$\overrightarrow{CF}$|=$\frac{\sqrt{3}}{2}$,
$\overrightarrow{AE}•\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$•$\overrightarrow{CA}$+$\frac{1}{4}$$\overrightarrow{CB}$•$\overrightarrow{CD}$-$\frac{1}{2}$${\overrightarrow{CA}}^{2}$-$\frac{1}{2}$$\overrightarrow{CA}$$•\overrightarrow{CD}$=-$\frac{1}{2}$,
∴cos<$\overrightarrow{AE}$,$\overrightarrow{CF}$>=$\frac{-\frac{1}{2}}{\frac{3}{4}}$=-$\frac{2}{3}$,
∴异面直线AE与CF所成角的余弦值为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$
点评 考查用空间向量求异面直线所成角余弦值的方法,等边三角形的中线也是高线,直角三角形的边角关系,以及向量加法的平行四边形法则,向量减法的几何意义,向量数量积的运算及计算公式,向量夹角的余弦公式,弄清异面直线所成角和异面直线的方向向量夹角的关系.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
| A. | {1} | B. | {4} | C. | {1,3} | D. | {1,4} |
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
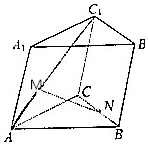 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).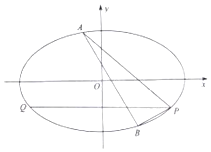 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)