题目内容
16.设正方体ABCD-A1B1C1D1的棱长为2,则点A1到平面B1AC的距离是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点A1到平面B1AC的距离.
解答 解: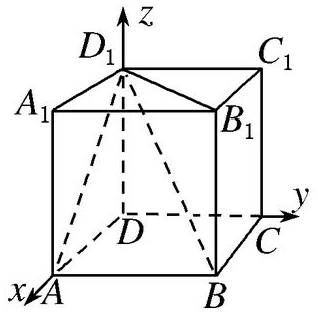 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A1(2,0,2),B1(2,2,2),A(2,0,0),C(0,2,0),
$\overrightarrow{A{B}_{1}}$=(0,2,2),$\overrightarrow{AC}$=(-2,2,0),$\overrightarrow{A{A}_{1}}$=(0,0,2),
设平面B1AC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=2y+2z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-2x+2y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,1,-1),
∴点A1到平面B1AC的距离:
d=$\frac{|\overrightarrow{A{A}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
∴点A1到平面B1AC的距离是$\frac{2\sqrt{3}}{3}$.
故选:D.
点评 本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
7.设函数f(x)=$\left\{\begin{array}{l}{2sinx,0≤x≤π}\\{{x}^{2},x<0}\end{array}\right.$,则函数y=f(f(x))-1的零点的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 无数个 |
4.已知A,B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A,B重合的动点.MN是圆O的一条直径,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是( )
| A. | [-$\frac{3}{4}$,0) | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,1] |
8.将圆周20等份,按照逆时针方向依次编号为1、2、…20,若从某一点开始,沿圆周逆时针方向行走,点的编号是数字几,就走几段弧长,称这种走法为一次“移位”,如:小明在编号为1的点,他应走1段弧长,即从1→2为第一次“移位”,这时他到达编号为2的点,然后从2→3→4为第二次“移位”,若某人从编号为3的点开始,沿逆时针方向,按上述“移位”方法行走,“移位”a次刚好到达编号为16的点,又满足|a-2016|的值最小,则a的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
6.集合A={x|x≤a},B={1,2},A∩B=∅,则a的取值范围为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
 如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点
如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点