题目内容
18．在（x2+2x+y）5的展开式中，x5y2的系数为60．分析 把（x2+2x+y）5化简成二项式机构，利用通项公式可得答案．
解答 解：由（x2+2x+y）5化简为[x2+2x）+y]，
由通项公式Tr+1=${C}_{5}^{r}{y}^{r}（{x}^{2}+2x）^{5-r}$，要出现y2，∴r=2．
二项式（x2+2x）3展开式中出现x5．
由通项公式Tk+1=${C}_{3}^{k}{x}^{2（3-k）}{2}^{k}{x}^{k}$，
∴2（3-k）+k=5，
可得：k=1．
∴x5y2的系数为${C}_{5}^{2}×2{×C}_{3}^{1}$=60．
故答案为：60．
点评 本题主要考查二项式定理对三项式的处理能力的应用，考查了二项式系数的性质，二项式展开式的通项公式，体现了转化的数学思想，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
6．已知复数Z为纯虚数，若（z+2）2-8i也是纯虚数，则Z的虚部为（ ）
| A． | 2 | B． | -2 | C． | -2i | D． | 2或-2 |
3．某程序框图如图所示，若输入的n=10，则输出结果为（ ）
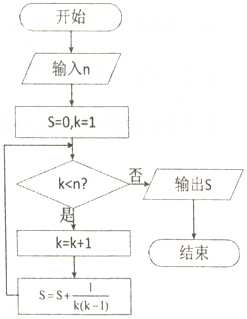
| A． | $\frac{1}{10}$ | B． | $\frac{8}{9}$ | C． | $\frac{9}{10}$ | D． | $\frac{10}{11}$ |
9．
菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水x（单位：千克） 清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克） 的统计表：
（1）在下面的坐标系中，描出散点图，并判断变量x与y的相关性；
（2）若用解析式$\widehaty=c{x^2}+d$作为蔬菜农药残量$\widehaty$与用水量x的回归方程，令ω=x2，计算平均值$\overlineω$与$\overline y$，完成以下表格（填在答题卡中），求出$\widehaty$与x的回归方程．（c，d精确到0.1）
（3）对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请
估计需要用多少千克的清水清洗一千克蔬菜？（精确到0.1，参考数据$\sqrt{5}≈2.236$）
（附：线性回归方程$\widehaty=bx+a$中系数计算公式分别为；$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）
菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水x（单位：千克） 清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克） 的统计表：| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
（2）若用解析式$\widehaty=c{x^2}+d$作为蔬菜农药残量$\widehaty$与用水量x的回归方程，令ω=x2，计算平均值$\overlineω$与$\overline y$，完成以下表格（填在答题卡中），求出$\widehaty$与x的回归方程．（c，d精确到0.1）
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ${ω_i}-\overlineω$ | -10 | -7 | -2 | 5 | 14 |
| ${y_i}-\overline y$ | 20 | 16 | 1 | -28 |
估计需要用多少千克的清水清洗一千克蔬菜？（精确到0.1，参考数据$\sqrt{5}≈2.236$）
（附：线性回归方程$\widehaty=bx+a$中系数计算公式分别为；$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）
10．椭圆的中心在坐标原点，焦点在x轴上，左右顶点分别为A1、A2，上下顶点分别为B1、B2，F2为右焦点，延长B2F2与A2B1交于点P，若∠B2PA2为钝角，则该椭圆离心率的取值范围是（ ）
| A． | $（{\frac{{\sqrt{5}-2}}{2}，0}）$ | B． | $（{0，\frac{{\sqrt{5}-2}}{2}}）$ | C． | $（{0，\frac{{\sqrt{5}-1}}{2}}）$ | D． | $（{\frac{{\sqrt{5}-1}}{2}，1}）$ |