题目内容
若曲线y=x4的一条切线l与直线x+4y-8=0垂直，则l的方程是（ ）
| A、4x-y-3=0 |
| B、x+4y-5=0 |
| C、4x-y+3=0 |
| D、x+4y+3=0 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：欲求l的方程，根据已知条件中：“切线l与直线x+4y-8=0垂直”可得出切线的斜率，故只须求出切点的坐标即可，故先利用导数求出在切点处的导函数值，再结合导数的几何意义即可求出切点坐标．从而问题解决．
解答：
解：设与直线x+4y-8=0垂直的直线l为：4x-y+m=0，
即曲线y=x4在某一点处的导数为4，
而y′=4x3，∴y=x4在（1，1）处导数为4，
将（1，1）代入4x-y+m=0，得m=-3，
故l的方程为4x-y-3=0．
故选A．
即曲线y=x4在某一点处的导数为4，
而y′=4x3，∴y=x4在（1，1）处导数为4，
将（1，1）代入4x-y+m=0，得m=-3，
故l的方程为4x-y-3=0．
故选A．
点评：本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．
练习册系列答案
相关题目
下列命题错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0” |
| B、若命题p：?x∈R，x2+x+1=0，则“?p”为：?x∈R，x2+x+1≠0 |
| C、“x＞2”是“x2-3x+2＞0”的充分不必要条件 |
| D、若“p∧q”为假命题，则p，q均为假命题 |
定积分
dx=（ ）
| ∫ | 2 0 |
| 4-x2 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
复数z=
（i为虚数单位）的共轭复数为（ ）
| 1+2i |
| i |
| A、2-i | B、2+i |
| C、-2+i | D、-2-i |
已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为（ ）
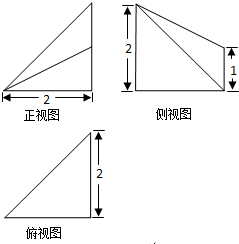
| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
已知集合A={x|
≥0}，集合B={y|y=sinx，x∈R}，则B∩CRA=（ ）
| 1+x |
| 1-x |
| A、∅ | B、{1} |
| C、{-1} | D、{-1，1} |
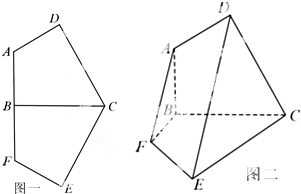已知轴对称平面五边形ADCEF（如图1），BC为对称轴，AD⊥CD，AD=AB=1，CD=BC=