题目内容
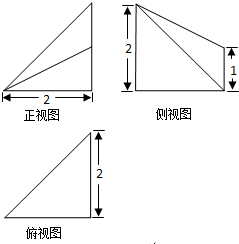
已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为（ ）
| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体为四棱锥，结合直观图判断棱锥的高与底面四边形的形状，判断相关几何量的数据，把数据代入棱锥的体积公式计算．
解答：
解：由三视图知：几何体为四棱锥，如图：
其中SA⊥平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，
∴四棱锥的体积V=
×
×2×2=2（cm3）．
故选：A．
其中SA⊥平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，
∴四棱锥的体积V=
| 1 |
| 3 |
| 1+2 |
| 2 |
故选：A．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的特征及相关几何量的数据是关键．
练习册系列答案
相关题目
sin（-150°）的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知集合M={x|-2＜x＜1}，N={x|-1＜x＜2}，则M∩N=（ ）
| A、{x|-2＜x＜2} |
| B、{x|-1＜x＜2} |
| C、{x|-1＜x＜1} |
| D、{x|-2＜x＜1} |
若曲线y=x4的一条切线l与直线x+4y-8=0垂直，则l的方程是（ ）
| A、4x-y-3=0 |
| B、x+4y-5=0 |
| C、4x-y+3=0 |
| D、x+4y+3=0 |
已知集合A={x|lg（x-2）＜1}，集合B={x|
＜2x＜8}，则A∩B等于（ ）
| 1 |
| 2 |
| A、（2，12） |
| B、（2，3） |
| C、（-1，3） |
| D、（-1，12） |
一个几何体的三视图如图所示，则这个几何体的体积等于（ ）
| A、90 | B、72 | C、68 | D、60 |
如图，已知A1，A2，B1，B2分别是椭圆C：