题目内容
9.已知a∈R,设命题p:指数函数y=ax(a>0且a≠1)在R上单调递增;命题q:函数y=ln(ax2-ax+1)的定义域为R,若“p且q”为假,“p或q”为真,求a的取值范围.分析 若“p且q”为假,“p或q”为真,则p与q一真一假,进而可得a的取值范围.
解答 解:若命题p为真命题,则a>1,
若命题q为真命题,
则ax2-ax+1>0恒成立,
即a=0或$\left\{\begin{array}{l}a>0\\△={a}^{2}-4a<0\end{array}\right.$.---4分;
所以0≤a<4…5分
若“p且q”为假,“p或q”为真,则p与q一真一假,
当p真q假时,a≥4.-------6分
当p假q真时,0≤a≤1.-------8分
综上可知,的取值范围为0≤a≤1或a≥4.-------10
点评 本题以命题的真假判断与应用为载体,考查了一无二次不等式恒成立问题,复合命题,难度中档.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.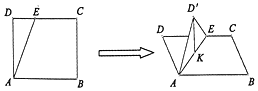 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
14.已知直线l1:(a+2)x+3y=5与直线l2:(a-1)x+2y=6平行,则a等于( )
| A. | -1 | B. | 7 | C. | $\frac{7}{5}$ | D. | 2 |
1.设f(x)是定义在R上的偶函数,对x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| A. | (2,3) | B. | $(\root{3}{3},2)$ | C. | $(\root{3}{4},2)$ | D. | $(\root{3}{2},3)$ |
18. 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=8,EF=5,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=8,EF=5,则AB与CD所成角的度数为( )
 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=8,EF=5,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=8,EF=5,则AB与CD所成角的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
19.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足|$\overrightarrow{b}$|=4|$\overrightarrow{a}$|,且$\overrightarrow{a}$⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
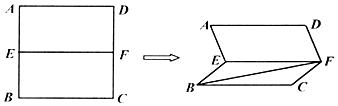 如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$. 如图,四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2.
如图,四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2.