题目内容
20.计算:(1)0.027${\;}^{-\frac{1}{3}}$-(-$\frac{1}{7}$)-2+256${\;}^{\frac{3}{4}}$-3-1+($\sqrt{2}$-1)0(2)${log_{2.5}}6.25+lg0.01+ln\sqrt{e}-{2^{1+{{log}_2}3}}$
(3)$lg{5}^{2}+\frac{2}{3}lg8+lg5•lg20+{(lg2)}^{2}$.
分析 (1)利用指数的运算法则即可得出.
(2)(3)利用对数的运算法则即可得出.
解答 解:(1)原式=$0.{3}^{3×(-\frac{1}{3})}$-7-1×(-2)+${4}^{4×\frac{3}{4}}$-$\frac{1}{3}$+1=$\frac{10}{3}$-49+64-$\frac{1}{3}$+1=19;
(2)原式=2-2+$\frac{1}{2}$-2×3=$-\frac{11}{2}$;
(3)原式=2(lg5+lg2)+lg5(lg2+1)+(lg2)2
=2+lg2(lg5+lg2)+lg5
=2+lg2+lg5
=3.
点评 本题考查了指数与对数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20.设集合A={0,1,2},B={x|(x+1)(x-2)<0},则A∩B的元素个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.若集合A={x|(x+4)(x+1)<0},集合B={x|x<-2},则A∩(∁RB)等于( )
| A. | (-2,-1) | B. | [-2,4) | C. | [-2,-1) | D. | ∅ |
9.有下列命题:(1)若z是复数,则|z|2=z2;(2)任意两个复数不能比较大小;(3)b2-4ac>0时,一元二次方程ax2+bx+c=0(a,b,c∈C)有两个不等的实数根,其中所有错误命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
10.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则该三棱锥S-ABC的外接球的表面积为( )
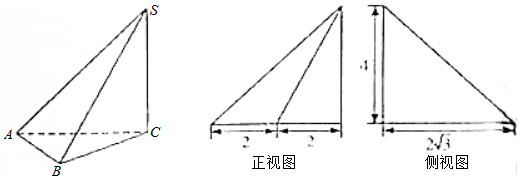

| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |